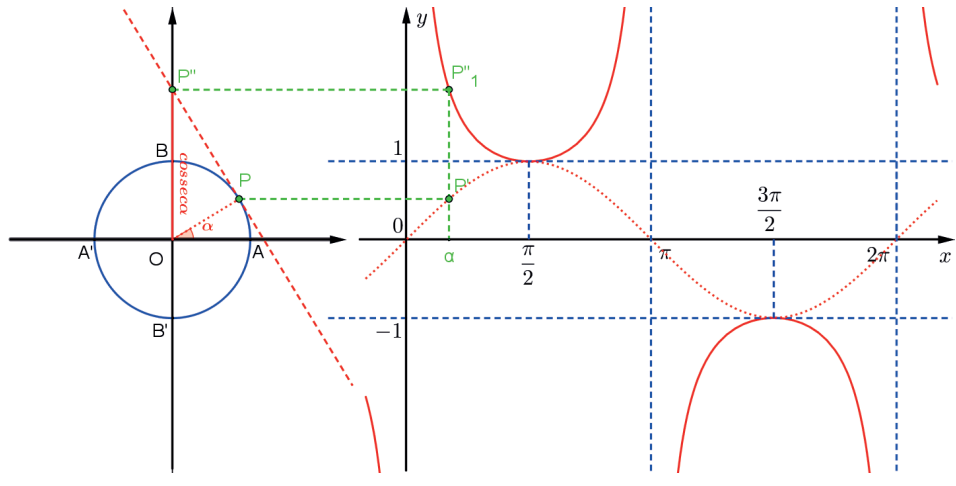
Seja θ um ângulo tal que θ ≠ k · π, k ∈ ℤ, e cuja imagem no ciclo trigonométrico é P. A cossecante de θ é a medida algébrica do segmento O̲P̲”, onde P” é a interseção da reta tangente ao ciclo trigonométrico em P com o eixo dos senos.
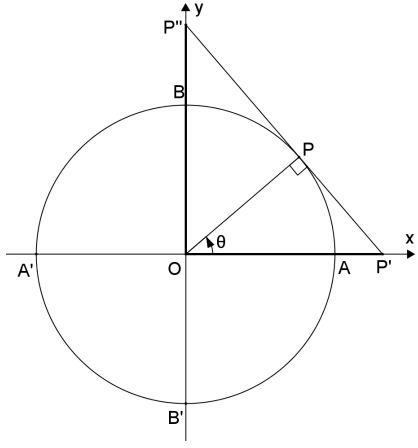
cossec θ = O̲P̲”
A função cossecante é a função de Dcossec em ℝ definida por f(x) = cossec x.
O domínio da função secante é Dcossec = {x ∈ ℝ ∣ x ≠ kπ, k ∈ ℤ} e a imagem Imcossec =]-∞,-1] ∪ [1,+∞[=ℝ-]-1,1[.
A função cossecante é periódica de período 2π.
Vamos analisar o gráfico da função cossecante, estudando os valores da cossecante de um ângulo de 0 a 2π. Assim, observe o que acontece com o segmento orientado O̲P̲”^ conforme o ponto P dá uma volta no ciclo trigonométrico.
1º) De A até B, ou seja, de θ = 0 (exclusive) até θ = π/2, a cossecante decresce de +∞ até f(π/2) = cossec π/2 = 1.
2º) De B até A’, ou seja, de θ = π/2 até θ = π (exclusive), a cossecante cresce de f (π/2) =cossec π/2 = 1 até +∞.
3º)$ De A’ até B’, ou seja, de θ=π (exclusive) até θ = 3π/2, a cossecante cresce de -∞ até f(3π/2) = cossec 3π/2 = -1.
4º) De B’ até A, ou seja, de θ = 3π/2 até θ=2π (exclusive), a cossecante decresce de f (3π/2) = cossec 3π/2 = -1 até -∞.