REFLEXÃO EM RELAÇÃO AO EIXO OX

AMPLITUDE
A função g(x) = sen x tem amplitude 1 e imagem Img = [-1,1]. A função f(x) = A sen x, com A > 0, tem amplitude A e imagem lmf = [-A,A].
Exemplo:
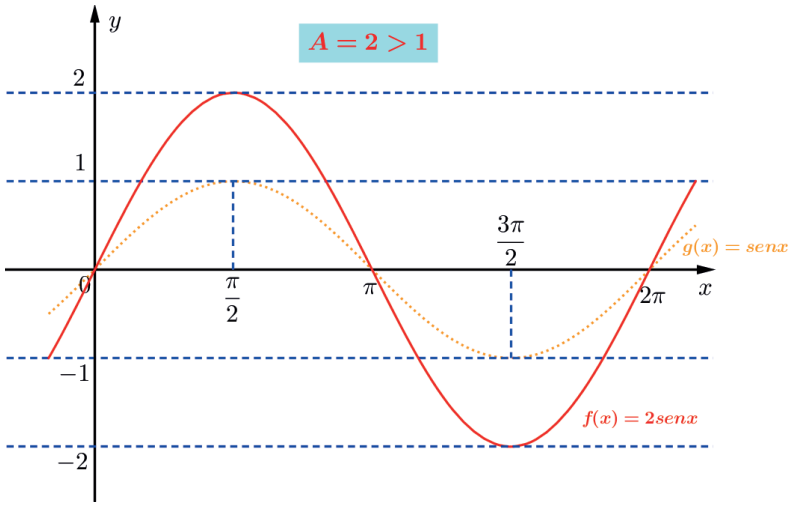
O gráfico da função f(x) = 2 sen x tem amplitude A = 2 e imagem Im = [-2, 2].
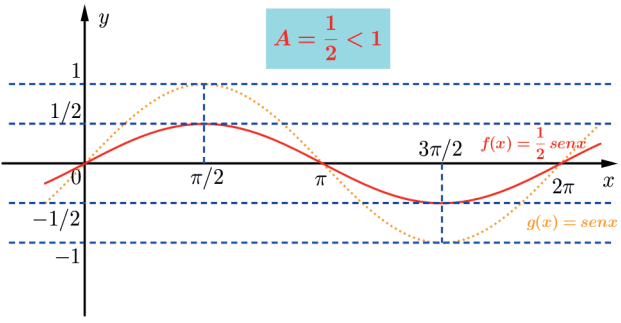
O gráfico da função f(x)= 1/2 sen x tem amplitude A = 1/2 e imagem Im = [ –1/2 , 1/2 ].
PERÍODO
A função f(x)=sen Bx possui período T = 2π/|B|.
Exemplo:
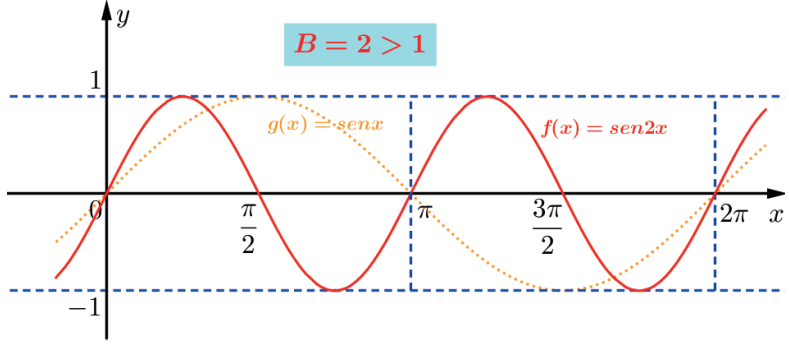
A função f(x)=sen 2x possui período T = 2π/2 = π.
Exemplo:
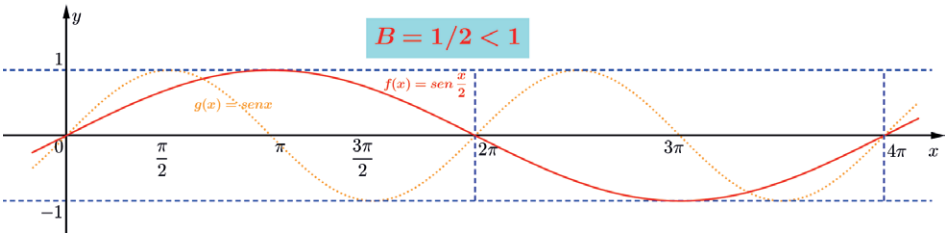
A função f (x) =sen x/2 possui período T = 2π/1/2 = 4π.
DESLOCAMENTO HORIZONTAL
O gráfico da função f(x)= sen (B x +C) é igual ao gráfico igual ao gráfico de g(x)=sen Bx deslocado na horizontal de – C/B. Se (- C/B) > 0, o gráfico se desloca para a direita e, se o gráfico se desloca para a esquerda.
Exemplo:
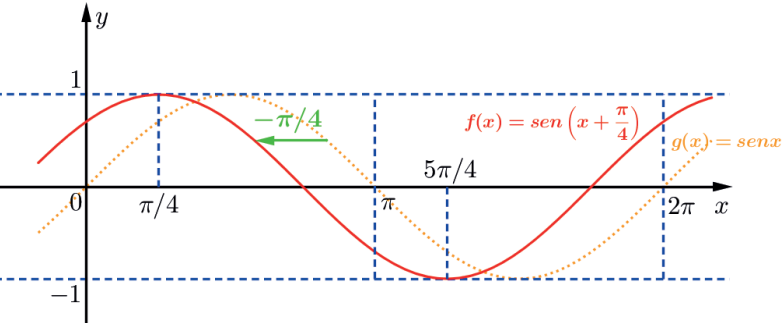
A função f(x) = sen (x + π/4) tem gráfico igual ao de f(x)= sen x deslocado de π/4 unidades para a esquerda.
Exemplo:
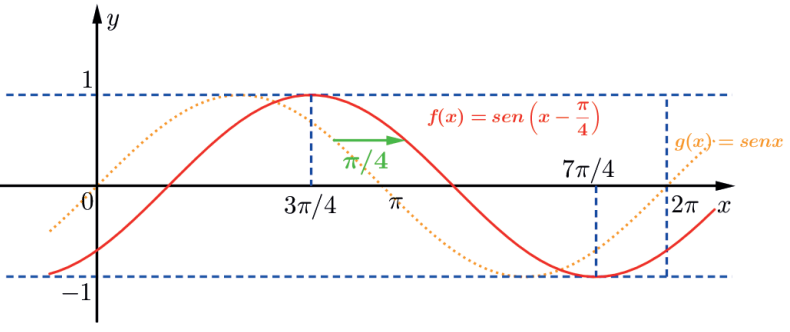
A função f(x) = sen (x – π/4) tem gráfico igual ao de f(x)=sen x deslocado de π/4 unidades para a direita.
Para encontrar o deslocamento na horizontal da função f(x)=sen (Bx + C), devemos fazer Bx + C = 0 ⇔ x = – C/B. Se 0 resultado for positivo, o deslocamento é para a direita e, se for negativo, o deslocamento é para a esquerda.
Exemplo:
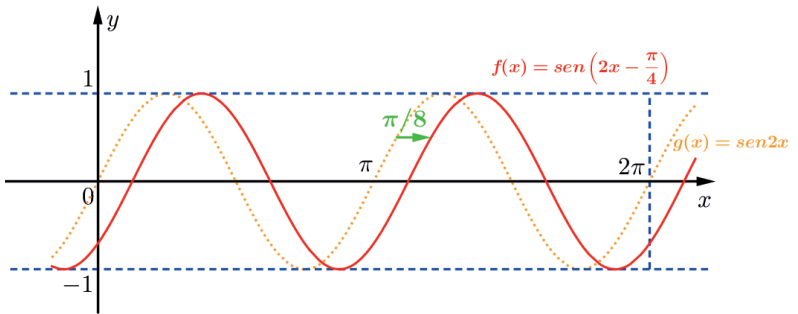
A função f(x) = sen (2x – π/4) tem gráfico igual ao de f(x)=senx deslocado de π/8 unidades para a direita.
DESLOCAMENTO VERTICAL
O gráfico da função f(x)= sen x + D é igual ao gráfico de f(x) = sen x deslocado na vertical de D unidades. Se D > 0, o gráfico se desloca para cima e, se D < 0, o gráfico se desloca para baixo.
Exemplo:
A função f(x) = sen x + 1 tem gráfico igual ao de g(x) = sen x deslocado de 1 unidade para cima.
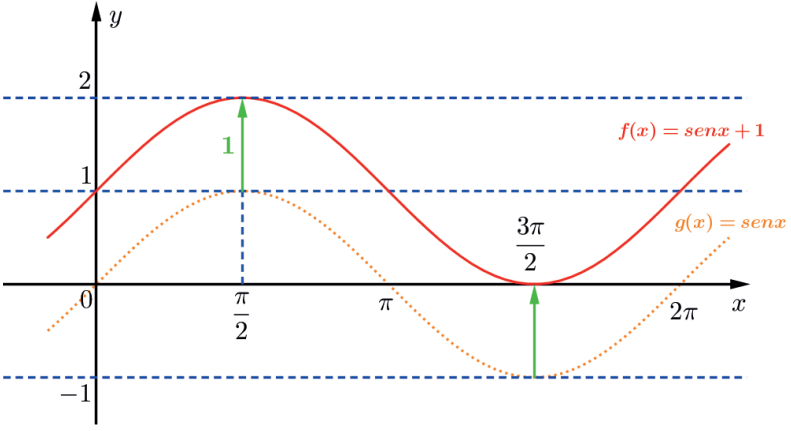
Exemplo:
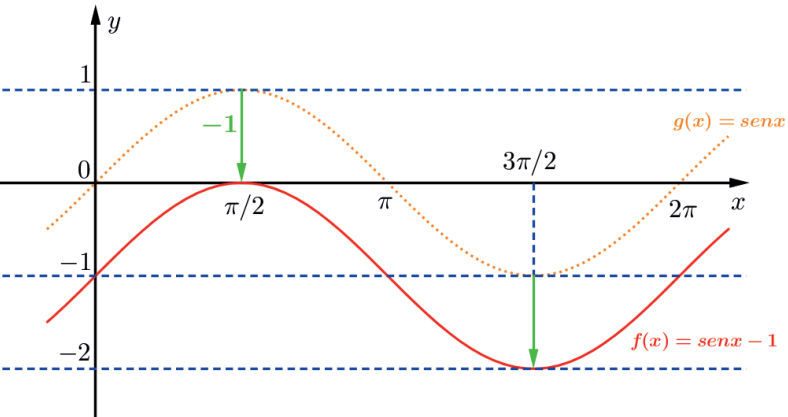
A função f(x)=sen x – 1 tem gráfico igual ao de g(x)=sen x deslocado de 1 unidade para baixo.
ProBizu
O gráfico de f(x) = Asen (B x + C) + D é tal que:
- |A| é a amplitude;
- T=2π/|B| é o período;
- (- C/B) é o número de fase, ou seja, o deslocamento na horizontal (para direita, se positivo, ou para a esquerda, se negativo); e
- D indica o deslocamento vertical (para cima, se positivo, ou para baixo, se negativo).
Exemplo:
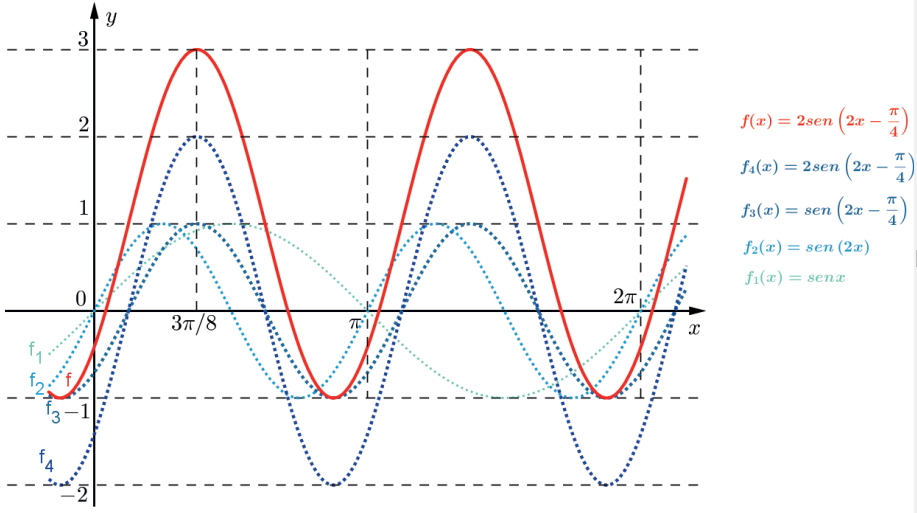
Construa o gráfico de f(x) = 2sen (2x – π/4)+1.
1º) Constrói-se f1(x) = sen x.
2º) Constrói-se f2(x) = sen 2x, a partir de f1, com período T = 2π/2 = π.
3º) Constrói-se f3(x) = sen (2x – π/4), a partir de f2 deslocando-se π/8 na horizontal para a direita.
4º) Constrói-se f4(x) = 2sen (2x – π/4), a partir de f3, com amplitude 2.
5º) Constrói-se f(x) = 2sen (2x – π/4) +1, a partir de f4, deslocando-se 1 na vertical para cima.