Funções: Inversa

A função inversa é um conceito matemático que descreve a relação reversa entre os valores de entrada e saída de uma função. Ela permite desfazer as transformações da função original, restabelecendo a correspondência original. Essa noção é crucial na resolução de equações e na compreensão de relações invertíveis em matemática e aplicações práticas.

Dados os conjuntos A={1,2,3,4} e B={1,3,5,7} consideremos a função f de A em B definida por f(x)=2 x-1.

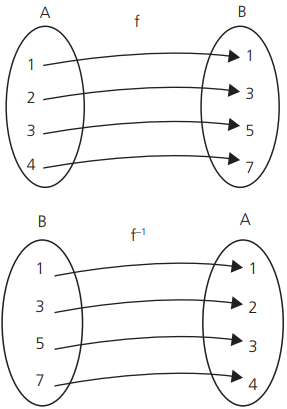
Notemos que f é bijetora formada pelos pares ordenados f={(1,1),(2,3),(3,5),(4,7)} onde D(f)=A e Im(f)=B.

A relação f-¹={(y,x)∣(x,y) ∈ f}, inversa de f, é também uma função, pois para todo y ∈ B existe x ∈ A.

A função inversa f-¹ é formada pelos pares {(1,1),(3,2),(5,3),(7,4)} onde D (f-¹) =B e Im (f-¹)=A.

Observemos que a função f é definida pela sentença y = 2x-1, e f-¹ pela sentença x = ^y+1/₂ isto é

a. f leva cada elemento x ∈ A até o y ∈ B tal que y = 2 x-1.

b . f-¹ leva cada elemento y ∈ B até o x ∈ A tal que x = ^y+1/₂ .

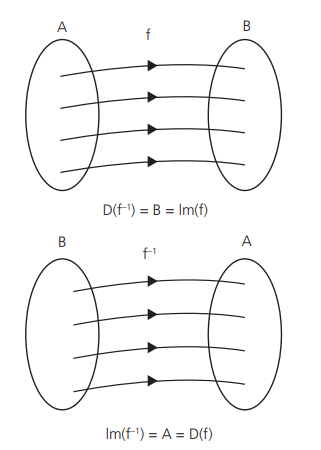
Obter a função inversa utilizando a regra prática.