FUNÇÃO INJETORA
Uma função f: A→B é considerada injetora se os elementos distintos de A tiverem imagens distintas em B.
f : A → B é injetora ⇔ (x1 ≠ x2 ⇒ f(x1) ≠ f(x2))
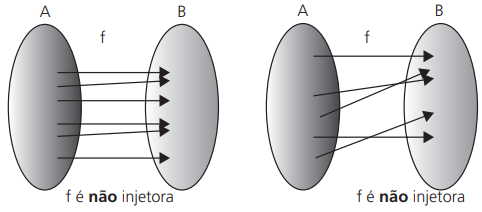
Uma função é considerada injetora no diagrama de flechas se cada elemento de B for atingido por no máximo uma flecha.
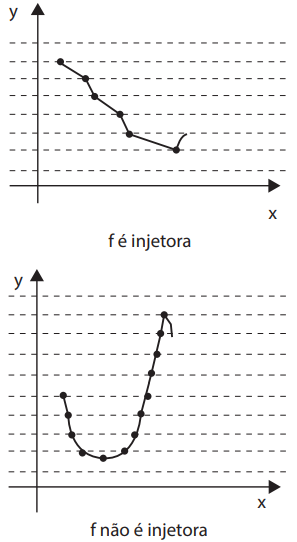
Uma função é considerada injetora no gráfico cartesiano se qualquer reta horizontal interrompe o gráfico, no máximo, uma vez.
FUNÇÃO SOBREJETORA
Uma função f: A→B somente é considerada sobrejetora quando o seu conjunto-imagem for igual ao contradomínio (B).
f : A → B é sobrejetora ⇔ If = CDf
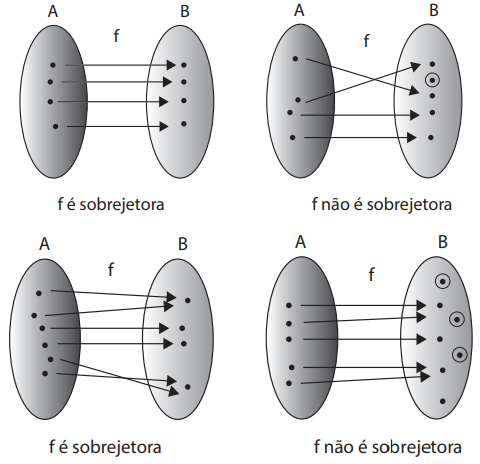
Uma função somente será sobrejetora em um diagrama de flechas se todos os elementos B forem atingidos por pelo menos uma flecha.
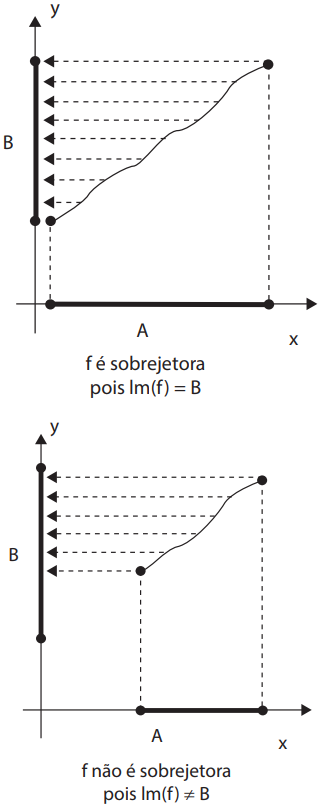
Uma função somente será sobrejetora em um plano cartesiano se a projeção do gráfico sobre o eixo Oy for contradomínio.
FUNÇÃO BIJETORA
Uma função f: A→B será considerada bijetora se f for sobrejetora e injetora.
Se cada uma das retas cortar o gráfico em um só ponto ou não cortar o Gráfico, será injetora.
a . f : ℝ→ℝ
f(x)=x
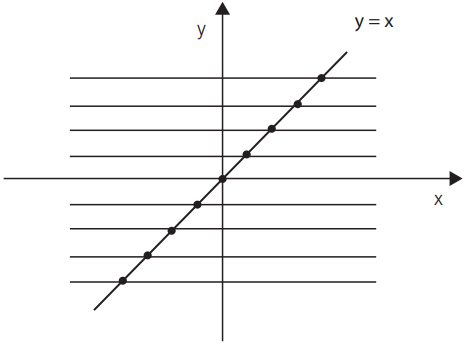
b . f : ℝ+→ℝ+
f(x)=x²
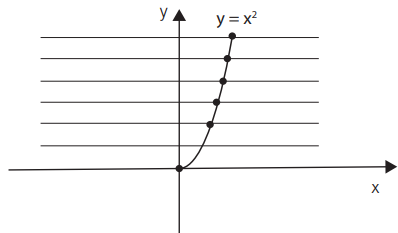
Se cada uma das retas cortar em um ou mais pontos, será sobrejetora.
a . f : ℝ→ℝ
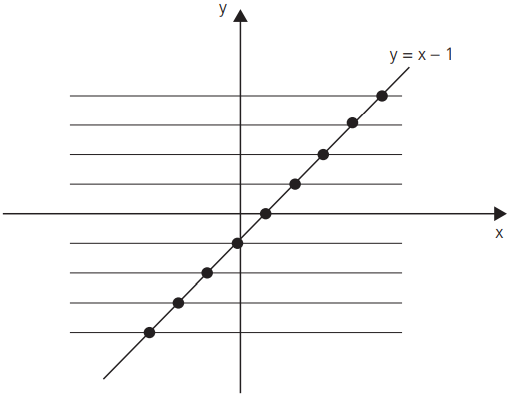
ProBizu: Para a função f(x)=x² se tivermos f : ℝ→ℝ+ ela será sobrejetora mas para f : ℝ→ℝ ela não será, pois para o caso f : ℝ→ℝ todos os números reais negativos estarão disponíveis no contra domínio mas não serão relacionados, logo sobrarão.
b . f : ℝ→ℝ+
f(x) = x²
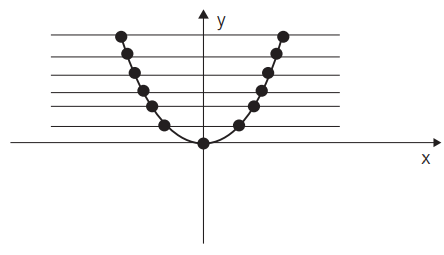
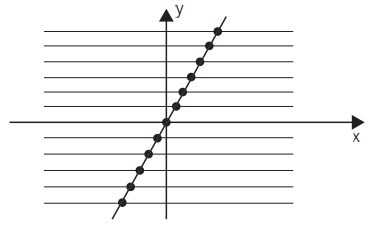
Se cada uma das retas cortar em um único ponto, será bijetora.
a . f: ℝ→ ℝ
f(x) = 2x
b . f : ℝ→ℝ
f(x)= x · |x|
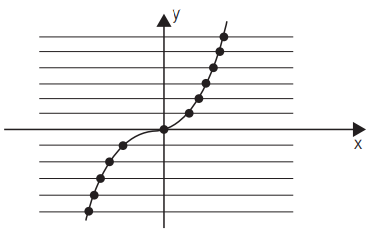
1. Se nenhuma reta corta o gráfico mais de uma vez f é injetora.
2. Se toda reta corta o gráfico, f é sobrejetora.
3. Se toda reta corta em um só ponto, f é bijetora.




