IMAGEM
O conjunto imagem de f de R em R definida por ax + b, com a ≠ 0, é R.
De fato qualquer que seja y∈R, existe x=y-b/a ∈R, (isolando x na equação y=a x+h).
COEFICIENTES DA FUNÇÃO AFIM
O coeficiente a da função f(x)=a x+b, é denominado coeficiente angular ou declividade da reta representada no plano cartesiano.
O coeficiente b da função f(x)=a x+b, recebe o nome de coeficiente linear.
Exemplo:
Na função f(x)=2 x+1 o coeficiente angular é 2 e o coeficiente linear é 1, observe que se x=0, temos, f(0)=2·0+1, f(0)=1, portanto para x=0, y=1.
Portanto, o coeficiente linear é a ordenada do ponto em que a reta corta o eixo y.
O coeficiente angular (a) é tangente do ângulo formado entre a reta e o eixo Ox→, vamos chamar esse ângulo de a.

ZERO DA FUNÇÃO AFIM
Zero de uma função é todo número x cuja imagem é nula, ou seja, f(x) = 0.
x é zero de y=f(x)⇔f(x)=0
Assim para determinarmos o zero da função afim, basta resolver a equação do primeiro grau a x+b=0, isolando x temos, a x=-b, passando a dividindo, x=- b/a .
Podemos interpretar graficamente o zero da função afim, como a abscissa do ponto onde o gráfico corta o eixo x.
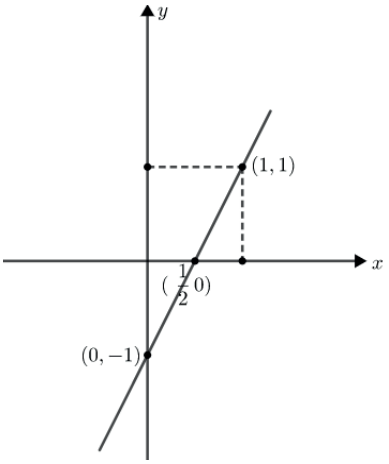
O zero desta função é 1/2, pois para x=1/2 temos y=0, (1/2, 0).
FUNÇÕES CRESCENTES OU DECRESCENTES
- f se diz uma função crescente se num intervalo x1 a x2, com x1<x2, temos fx1<fx2.
- Ou seja, se num intervalo x cresce, as imagens f(x) crescem também.
- f se diz uma função decrescente se num intervalo x1 a x2, com x1<x2, temos fx1>fx2
Ou seja, se num intervalo x cresce, as imagens f(x) decrescem.
Teorema: Uma função afim é crescente se o seu coeficiente angular (a) é positivo e é decrescente se o coeficiente angular é negativo.
SINAL DA FUNÇÃO AFIM
Como já vimos o zero da função é x=- b/a.
Caso 1: se a > 0 (função crescente).
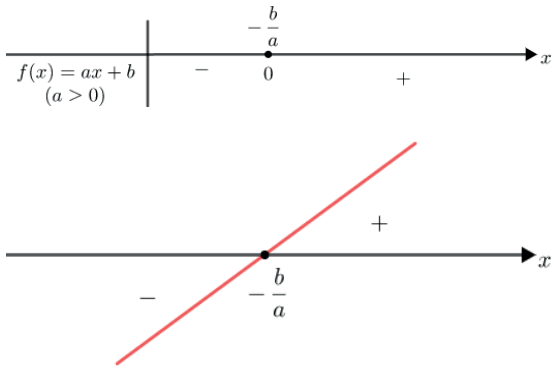
Caso 2: se a < 0, (função decrescente).
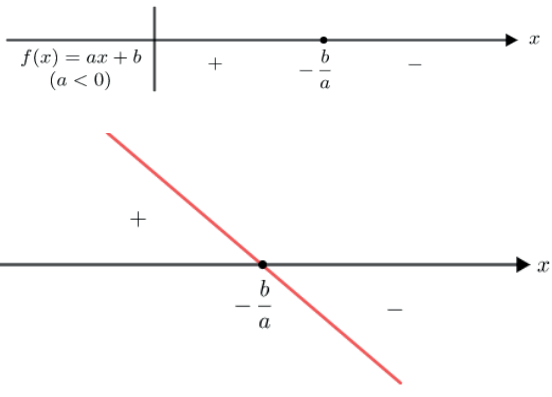
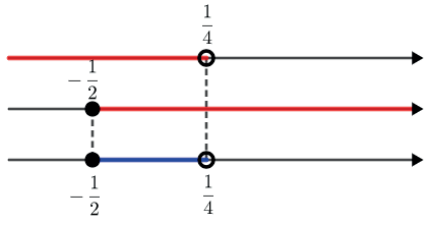
NEQUAÇÕES SIMULTÂNEAS
A dupla desigualdade f(x) < g(x) < h(x), se decompõem em 2 inequações simultâneas.

Exemplo:

Temos que resolver as 2 inequações:

A interseção desses dois conjuntos é: