Um representante comercial recebe, mensalmente, um salário composto de duas partes: uma parte fixa, no valor de R$ 2500,00 e uma parte variável, que corresponde a uma comissão de 6% (0,06) sobre o total das vendas que ele faz durante o mês. Observe que o salário desse vendedor é dado em função do total de vendas que ele faz durante o mês.
Representando o total de venda por x, temos: s(x) = 2500,00 + 0,06x ou s(x) = 0,06x + 2500,00 ou y = 0,06x + 2500,00. Esse é um exemplo de função afim.
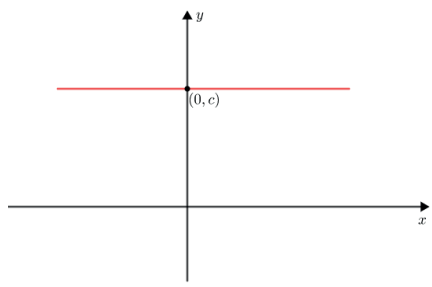
FUNÇÃO CONSTANTE
Uma aplicação f de R em R recebe o nome de função constante quando a cada elemento x ∈ R associa sempre o mesmo elemento c ∈ R.
f : R ➝ R
x ➝ c
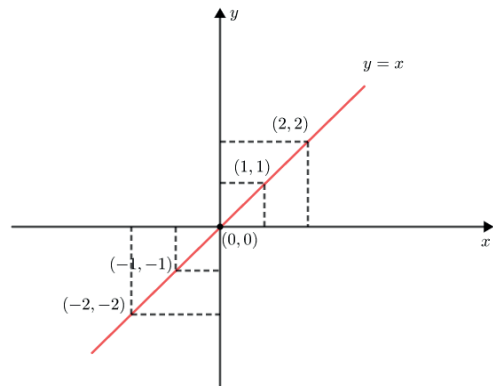
FUNÇÃO IDENTIDADE
Uma aplicação f de R em R recebe o nome de função identidade quando a cada elemento x ∈ R associa o próprio x.
f : R ➝ R
x ➝ c
FUNÇÃO LINEAR
Uma aplicação f de R em R recebe o nome de função linear quando a cada elemento x∈R associa elemento ax ∈ R, onde a ≠ 0 é um número real dado.
f : R ➝ R
x ➝ ax, a ≠ 0
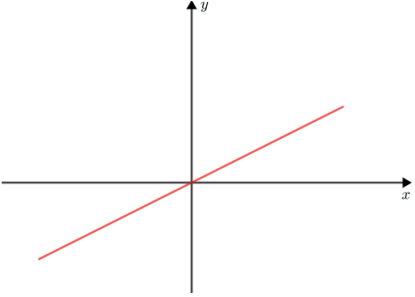
O gráfico da função linear é uma reta que sempre passa pela origem.
FUNÇÃO AFIM
Uma aplicação f de R em R recebe o nome de função afim quando a cada elemento x ∈ R associa (ax + b) ∈ R com a ≠ 0.
f:R→R
x→ax+b, a≠0
Exemplos:
y = 3x + 2, onde a = 3 e b = 2
y = –2x + 1, onde a = –2 e b = 1
y = x – 3, onde a = 1e b = –3
y = 4x, onde a = 4 e b = 0
Repare que para b = 0 teremos, f(x) = ax que é uma função linear, então, a função linear é um caso particular da função afim.
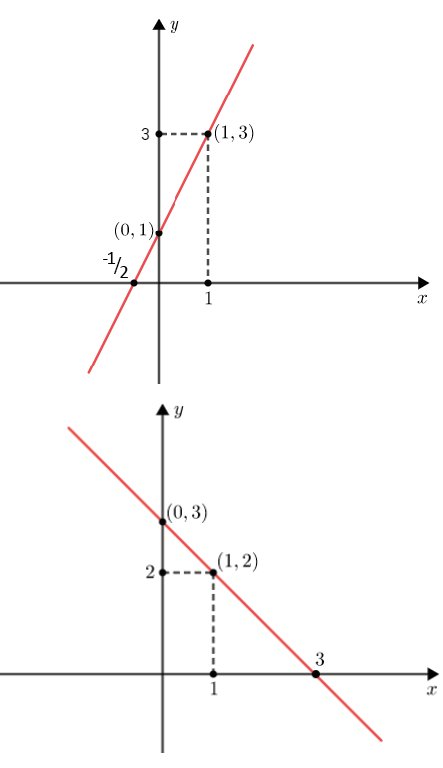
GRÁFICO
O gráfico cartesiano da função f(x) = ax + b, com a ≠ 0, é uma reta.
f(x) = 2x + 1