RELAÇÕES
Par ordenado: conjunto ordenado de dois elementos, representado pelo símbolo (x,y) onde x e y são números reais, denominados respectivamente de abscissa e ordenada.
Exemplo: Par ordenado (6,–3) abscissas = 6 e ordenada = – 3.
Propriedade: dois pares ordenados são iguais, quando são respectivamente iguais as abscissas e as ordenadas. Em termos simbólicos: (x;y) = (w;z) ↔ x = w e y = z
PLANO CARTESIANO
Também conhecido como sistema de coordenadas retangulares, consiste basicamente de dois eixos orientados que se interceptam segundo um angulo reto, num ponto denominado origem. O eixo horizontal é denominado eixo das abscissas e o eixo vertical é denominado eixo das ordenadas. Denominamos o ponto O de origem do plano cartesiano, sendo nulas a sua abscissa e a sua ordenada, ou seja, O(0;0).
PRODUTO CARTESIANO
Produto cartesiano é um uma operação entre conjuntos representada por A×B (Lê-se: A cartesiano B). O resultado da operação cartesiano é um conjunto de pontos que obedecem às condições:
A×B={(x,y)/x∈A e y∈B}
B×A={(x,y)/x∈B e y∈A}
Note que na operação cartesiano, a abscissa (x) sempre sai do primeiro conjunto da operação enquanto a ordenada (y) sempre sai do segundo conjunto da operação.
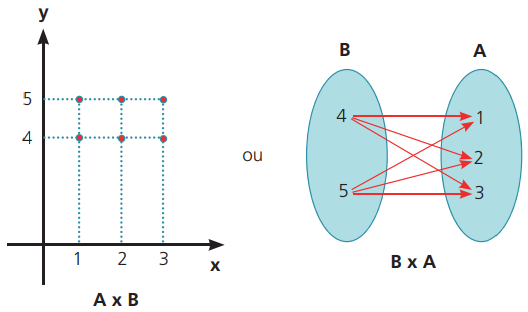
Exemplo: sejam os conjuntos A={1,2,3} e B=(4,5}. Determine A×B e B×A.
Para achar o produto cartesiano entre A e B, basta montar todos os possíveis pontos em que a coordenada x pertence ao conjunto A e a coordenada y pertence ao conjunto B.
A×B={(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)}
Para achar o produto cartesiano entre B e A, basta montar todos os possíveis pontos em que a coordenada x pertence ao conjunto B e a coordenada y pertence ao conjunto A.
B×A={(4,1),(4,2),(4,3),(5,1),(5,2),(5,3)}
Propriedades
Como pudemos observar no exemplo anterior, na operação cartesiano, a ordem dos conjuntos altera o resultado final, ou seja, A×B≠B×A. No entanto, quando A=B, temos que A×B=B×A.
Além disso, o número de elementos de um produto cartesiano sempre pode ser encontrado multiplicando a quantidade de elementos do primeiro conjunto pela quantidade de elementos do segundo conjunto.
n(A×B)=n(A)·n(B)=n(B×A)
Representação
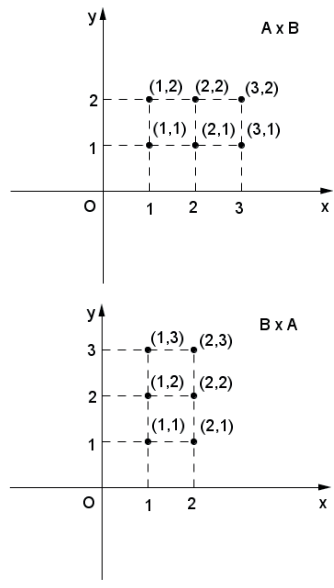
Exemplo:
A={1,2,3} e B = {1,2}
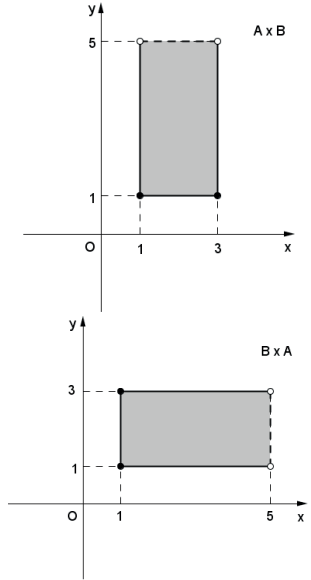
Exemplo:
A=[1,3] e B=[1,5]
PRODUTOS CARTESIANOS ESPECIAIS
ℕ²=ℕ×ℕ é o conjunto de todos os pontos em que a abscissa e a ordenada são números naturais.
ℤ²=ℤ×ℤ é o conjunto de todos os pontos em que a abscissa e a ordenada são números inteiros.
ℝ²=ℝ×ℝ é o conjunto de todos os pontos em que a abscissa e a ordenada são números reais.




