FUNÇÃO
Para definir uma função, necessitamos de dois conjuntos (Domínio e Contradomínio) e de uma fórmula ou uma lei que relacione cada elemento do domínio a um e somente um elemento do contradomínio.
Nota: Então para uma relação ser uma função, devemos ter o seguinte: que não sobre nenhum elemento no conjunto A ou conjunto de partida (domínio) sem se relacionar com um elemento do conjunto B e que um mesmo elemento do conjunto A se relacione com dois elementos do conjunto B.
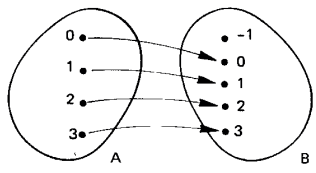
Como no exemplo acima.
Os exemplos abaixo não se tratam de uma função
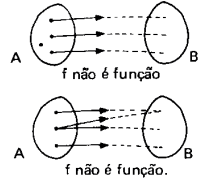
No primeiro está sobrando um elemento no conjunto A (domínio) sem se relacionar com algum elemento de B (contradomínio). E no segundo dois elementos do conjunto A estão se relacionando com um único elemento de B.
Exemplo: qual das relações abaixo é uma função?
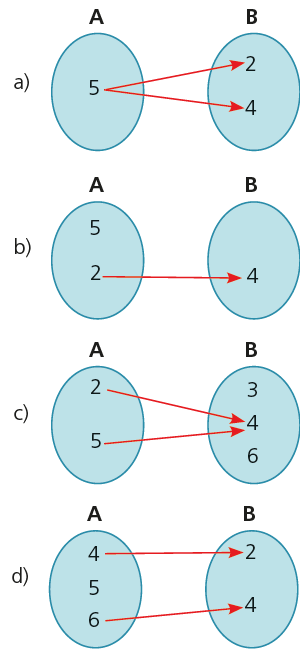
Resolução: C
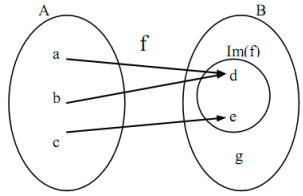
a) O elemento 5 possui 2 imagens. Não é função.
b) O elemento 5 não possui imagem. Não é função.
c) Todos os elementos de A possuem uma única imagem em B. É função.
d) O elemento 5 não possui imagem. Não é função.
Repare que a análise feita no diagrama de conjuntos é relativamente simples, porém, a análise no plano cartesiano funciona de forma um pouco diferente, observe abaixo.
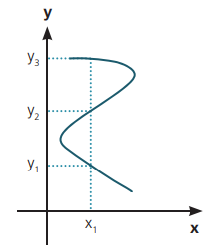
No gráfico acima, podemos ver que $x_1$ possui três imagens, y1,y2 e y3. Logo, não é função.
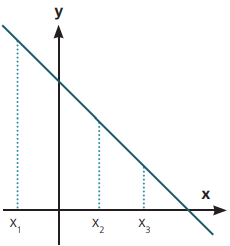
No gráfico acima, podemos ver que x1,x2 e x3 possuem, cada um, uma única imagem. Logo, é função.
Na prática, para verificar se um gráfico é ou não função, basta traçar retas verticais ao longo do eixo horizontal (x). Se todas as retas interceptarem a função em apenas um ponto, então é função. Se alguma das retas interceptar o gráfico em menos de um ponto ou mais de um ponto, então não é função.
DOMÍNIO E IMAGEM
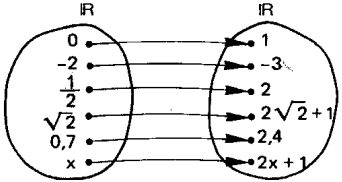
No exemplo acima temos dois conjuntos e uma regra que relaciona os elementos desses conjuntos. Nesse exemplo se trata de uma função, pois no conjunto A não sobra nenhum elemento e dois elementos de A não possuem um mesmo correspondente em B.
Chamamos o conjunto de partida de domínio da função, o conjunto de chegada das setas de contradomínio, e cada elemento do contradomínio de imagem. Então por exemplo, 1 é a imagem do elemento 0, 2 é a imagem do elemento 1/2. E temos que a regra dessa função é 2x+1, ou seja, cada elemento de A é multiplicado por 2 e somado uma unidade para resultar na sua imagem que pertence a B ou ao contradomínio.
Em algumas situações, o domínio e o contradomínio não estarão explícitos, sendo apresentada somente a lei de formação. Nesses casos, consideremos que o domínio seja o maior subconjunto possível dos números reais (D⊂R) para o qual a lei faça sentido.
Exemplo: f(x)= √x, como não existe raiz quadrada de um número negativo no conjunto dos números reais, consideremos que o domínio seja o conjunto dos números reais não negativos, para poder haver a operação da raiz quadrada.
D(f) = R+ ou D(f) = {x ∈ R ∣ x ≥ 0}
Exemplos:
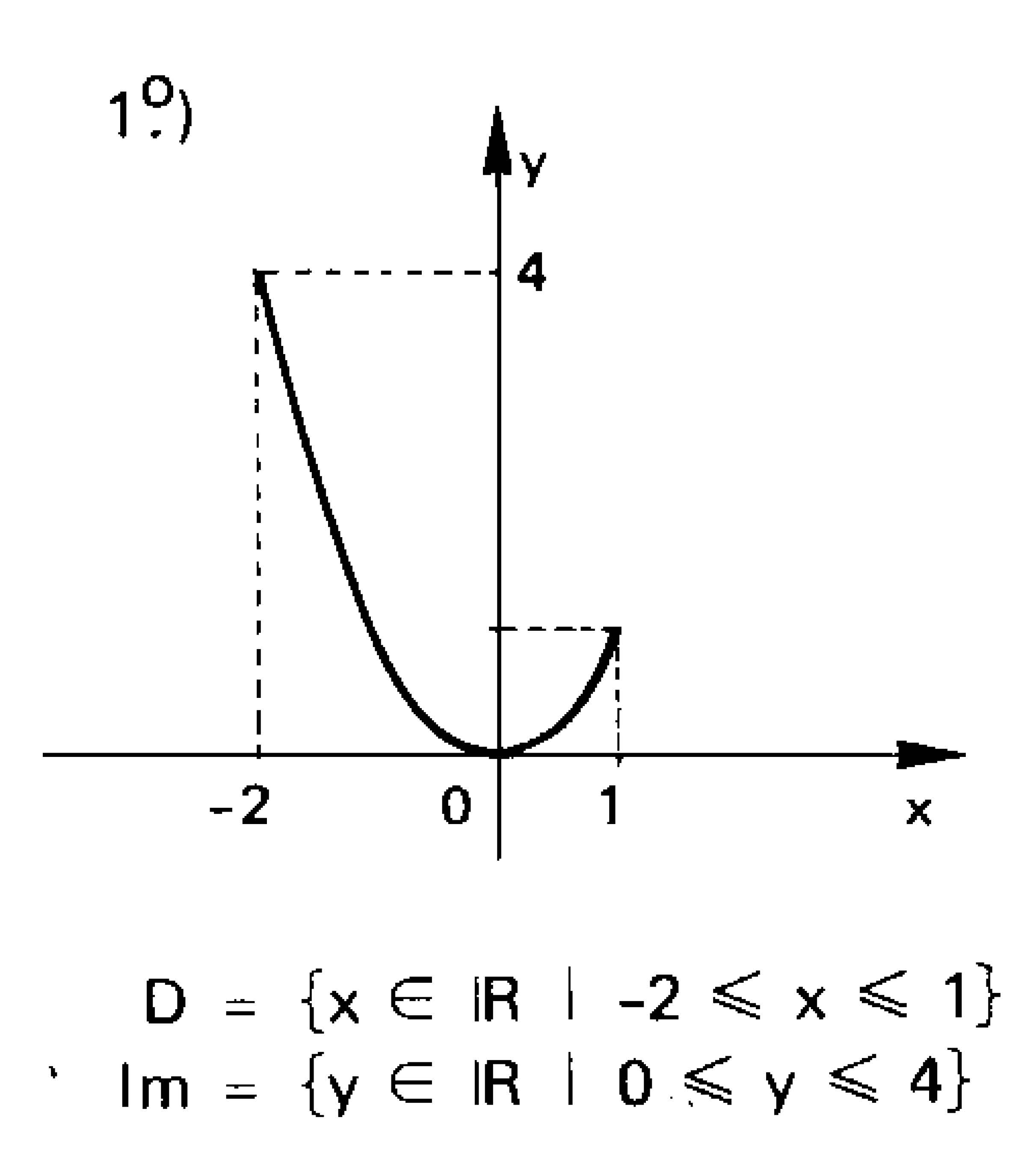
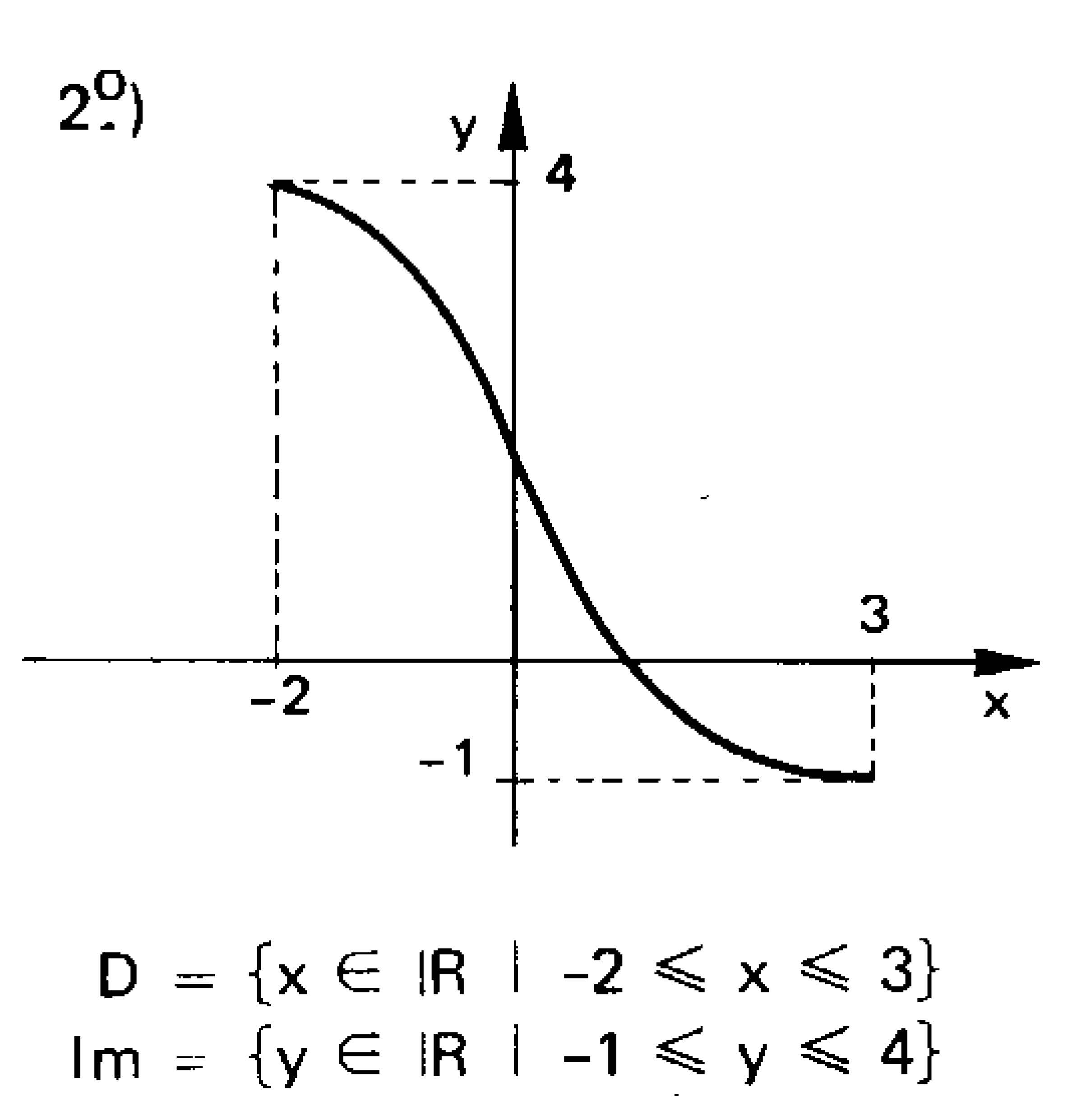
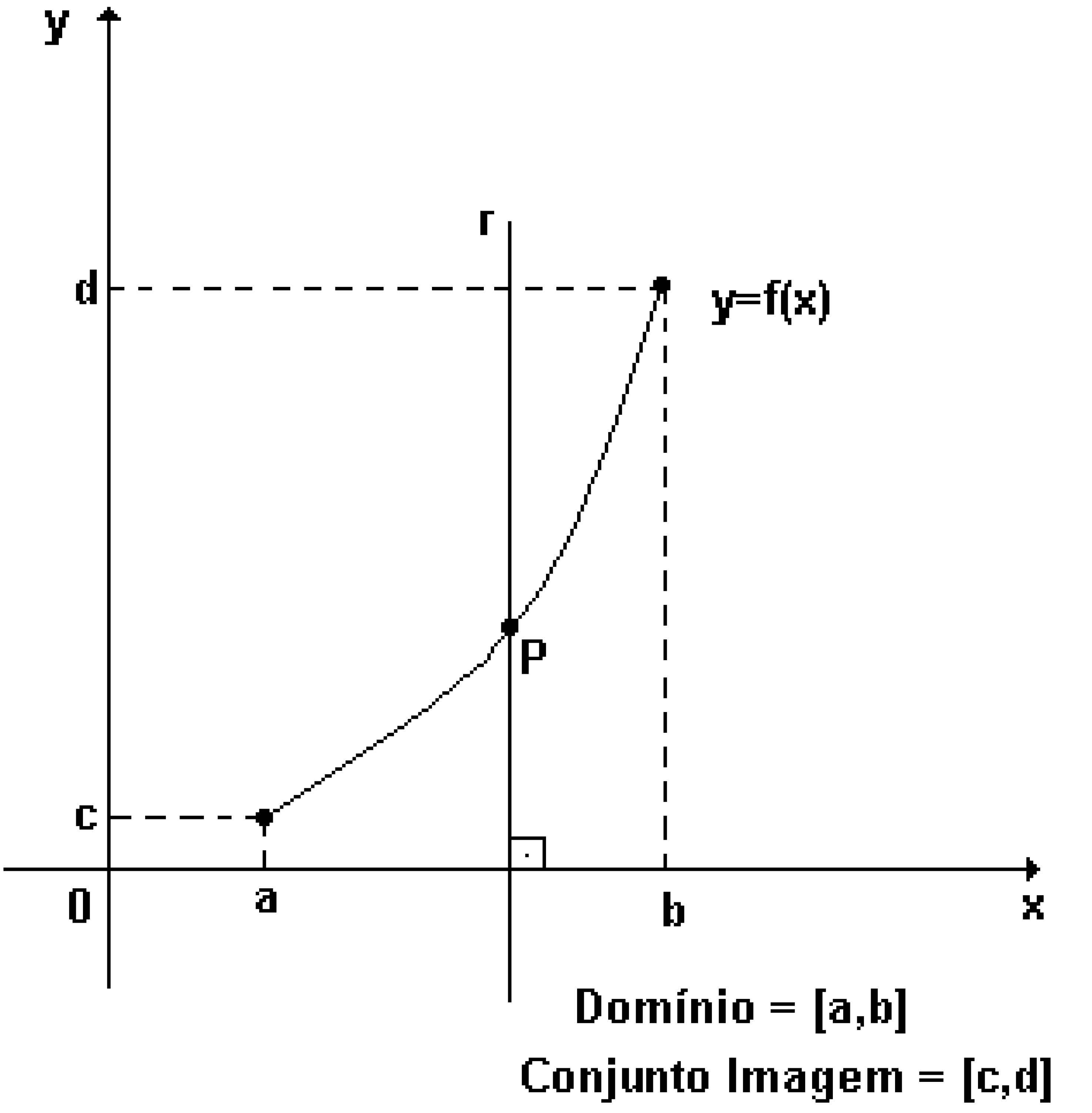
NOTAÇÃO
Notação é a forma como escrevemos a função. É preciso estar familiarizado com a forma de escrever as funções, já que é comum observar esse tipo de notação nas questões.
Exemplo:
f : A → B
x → f(x) = x² + 1
f: Nome da função. Podemos usar qualquer letra, mas é comum trabalhar com a letra f.
A: Domínio da função f. Conjunto de onde saem os valores de x.
B: Contradomínio da função f. Conjunto de onde saem os valores de y.
f(x)= x² + 1: Lei de formação. É a expressão algébrica que relaciona os valores de x e y. A lei de formação é uma forma de acharmos os pontos que compõe o gráfico da função f, transformando os valores de x do conjunto A em valores de y do conjunto B.




