FUNÇÃO COMPOSTA
Considere as funções f : A → B e g : B → C, estas são funções compotas das funções de g e f à função h : A → C tal que h(x) = g [f(x)]
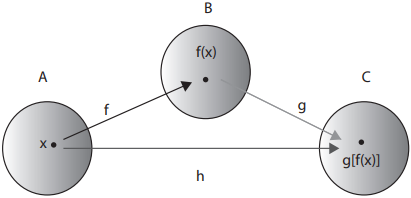
A função h : A → C, composta de g e f, é indicada por gof ou por g(f(x)).
Interpretado por: g bola f.
Desse modo: h(x)=(g∘f)(x)=g[f(x)]
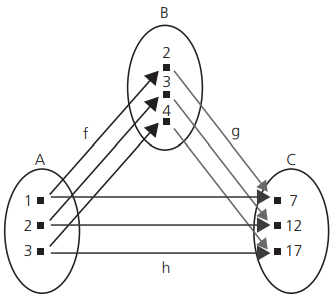
Exemplos: considere os conjuntos A={2,3,5}, B={5,7,8} e C={4,6,9} e as funções
f: A → B e g: B → C definidas por f(x)=x + 1 e g(x)=5x – 3.
f(2) = 5 e g(5) = 4
f(3) = 7 e g(7) = 6
f(5) = 8 e g(8) = 9
A função h : A → C, composta de g e f, onde h(x) = (g∘f) é tal que:
h(2)=(g ∘ f)(2)=g[f(2)]=g(5)=4
h(3)=(g ∘ f)(3)=g[f(3)]=g(7)=6
h(5)=(g ∘ f)(5)=g[f(5)]=g(8)=9
Observação:
- A imagem de um determinado elemento x de A através da função composta gof é definida em duas partes: A transformação do elemento x de A no elemento f(x) de B.
- A transformação do elemento f(x) de B no elemento g[f(x)]=(g ∘ f)(x) de C.
- O contradomínio de f é idêntico ao domínio de g, porém, para existir gof é preciso que Im (f) ⊂ D (g).




