DEFINIÇÃO
É uma função da forma f(x) = ax2 + bx + c, com a, b, c ∈ ℝ e a ≠ 0.
Observação: a é dito coeficiente líder da função quadrática.
Exemplo: f(x) = 4x2 + 5x – 8.
GRÁFICO
O gráfico de uma função quadrática é uma parábola.
Observação: quando a > 0, a parábola tem concavidade voltada para CIMA e quando a < 0, a parábola tem concavidade voltada para BAIXO.
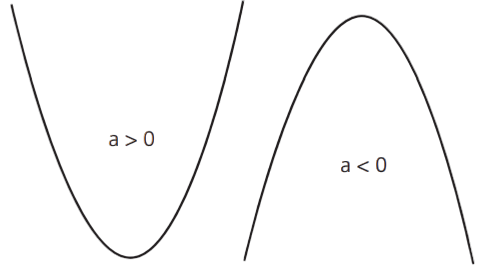
ProBizu: para memorizar mais facilmente a concavidade da parábola, podemos pensar no seguinte “macete”: Quando a > 0, pensamos que “a parábola está feliz” e assim a concavidade é para CIMA. Quando a < 0, pensamos que “a parábola está triste” e assim a concavidade é para BAIXO.
RAÍZES
Para resolver uma equação da forma ax2 + bx + c = 0 usaremos a técnica de completar quadrados, vista no nosso módulo de fatoração:
ax2 + bx + c = 0 ⇔ 4a2x2 + 4abx + 4ac = 0
Somando b2 – 4ac a ambos os lados, temos que (2ax + b)2 = b2 – 4ac. Sendo b2 – 4ac = Δ (discriminante), obtemos a “Fórmula de Bhaskara”. As raízes da equação do 2º grau ax2 + bx + c = 0, a ≠ 0, são dadas por -b±√Δ/2a , onde Δ = b2 – 4ac.
Observação: a fórmula de Bhaskara também é verdadeira para equações com coeficientes complexos.
INTERSECÇÃO DA COM EIXO Oy↔
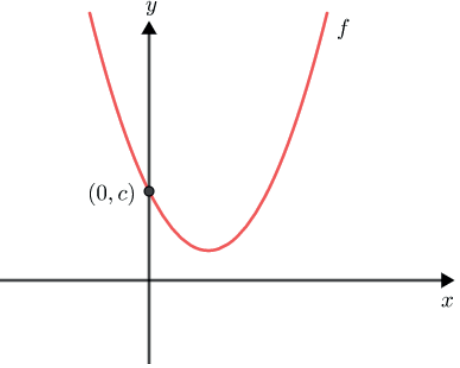
Quando buscamos a intersecção com o eixo Oy↔ estamos buscando o ponto da forma (0, f0), ou seja, o valor da função f para x = 0. Dessa forma temos f0 = a · 02 + 0 · x + c, portanto o potno em que a parábola corta o exio das ordenadas é o ponto (0, c).
DISCUSSÃO SOBRE AS RAÍZES REAIS
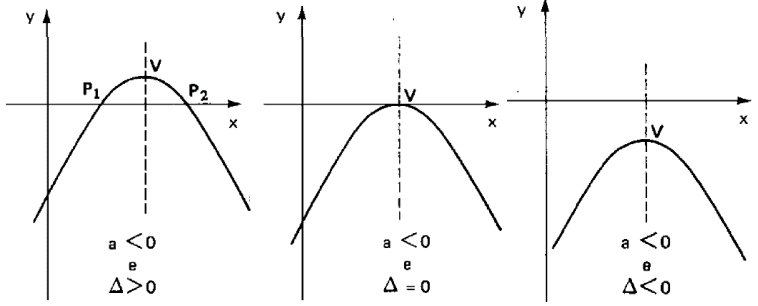
Dada uma equação do 2º grau com coeficientes reais, temos:
I. Δ > 0: a equação possui duas raízes reais distintas.
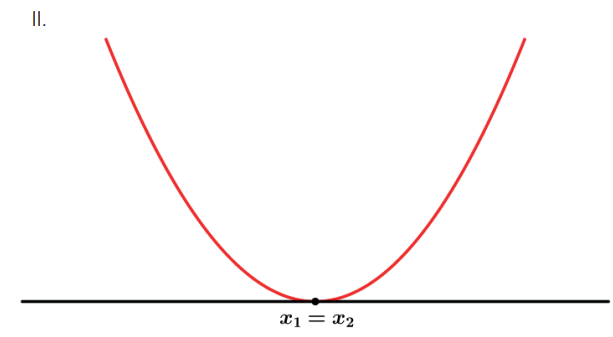
II. Δ = 0: a equação possui duas raízes reais iguais (raiz dupla).
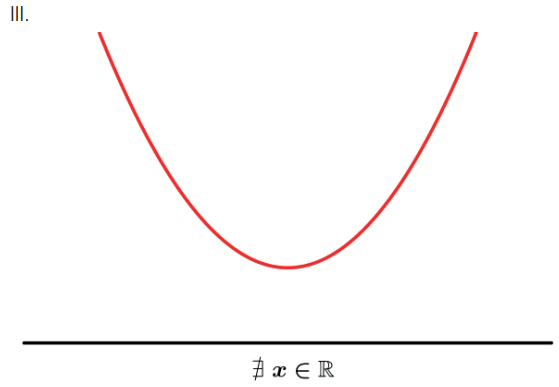
III. Δ < 0: a equação não possui raízes reais.
Cada sinal do determinante irá determinar uma maneira diferente que a parábola pode ou não interceptar o eixo Ox↔.
RELAÇÕES ENTRE COEFICIENTES E RAÍZES
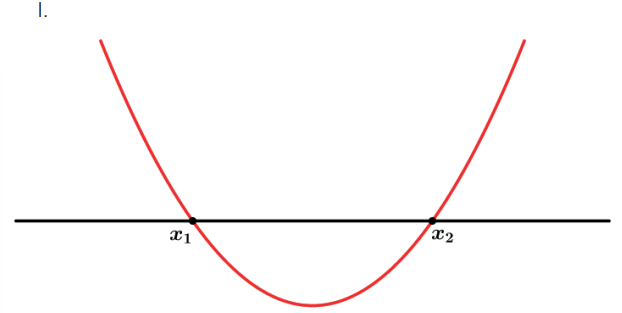
Dada uma equação do segundo grau ax2 + bx + c = 0 de raízes x1 e x 2 , temos que S = x1 + x2 = –b/a ,P = x1x2 = c/a.
Para demonstrarmos estas fórmulas, basta usar a fórmula de Bhaskara:
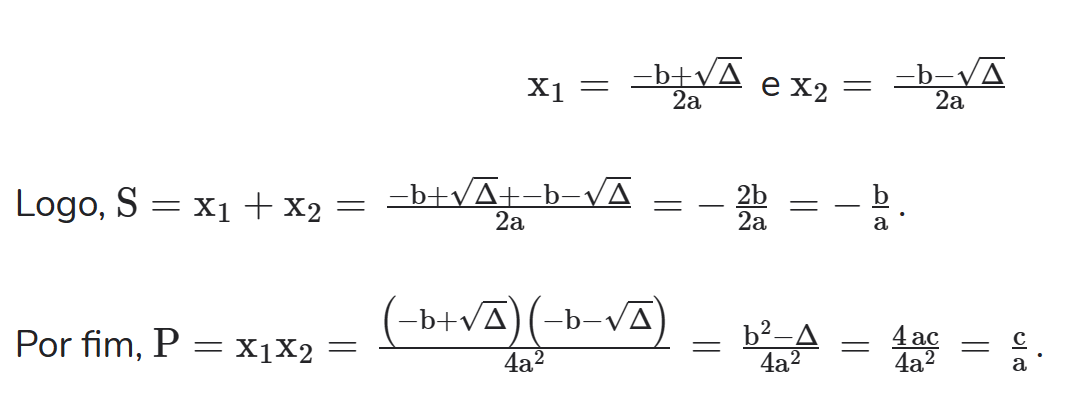
ProBizu: fique atento às seguintes ideais que despencam em prova:
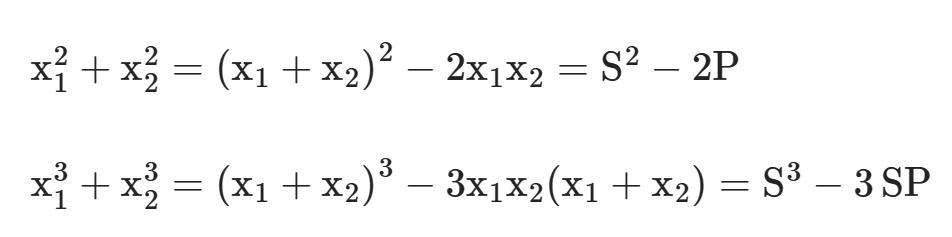
MÁXIMOS E MÍNIMOS
Muitos problemas que aparecem nas provas militares envolvem minimizar ou maximizar uma função quadrática. Vejamos agora como calcular os máximos e mínimos de uma função quadrática:
I. Se a > 0, a função quadrática y = ax2 + bx + c admite valor mínimo yv = – Δ/4a (“y do vértice”) e tal valor mínimo ocorre para x = xv = – b/2a (“x do vértice”). Neste caso, o “x do vértice” é dito minimizante.
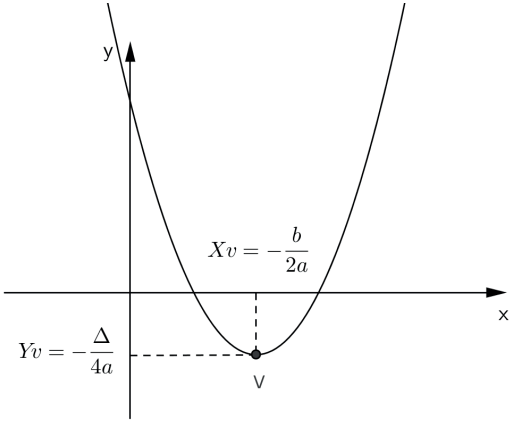
II. Se a < 0, a função quadrática y = ax2 + bx + c admite valor máximo yv = – Δ/4a (“y do vértice”) e tal valor máximo ocorre para x = xv = – b/2a (“x do vértice”). Neste caso, o “x do vértice” é dito maximizante.
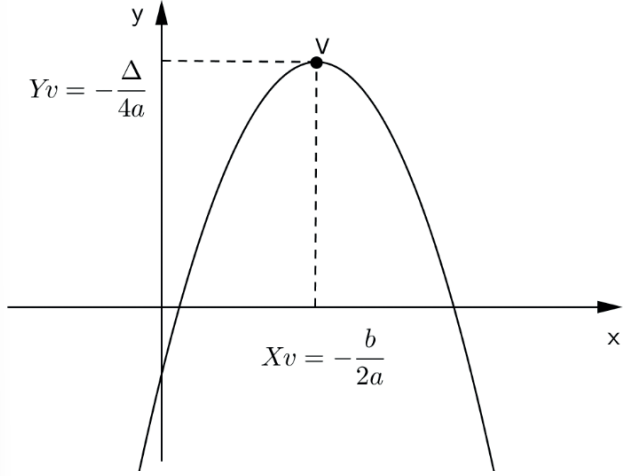
Observação:
Sabemos que 2 m + n = 8, com m e n números reais. Devemos determinar o par (m, n) que torna o produto m · n máximo.
Veja que podemos isolar n em função de m.
n = 8 – 2 m
Acabamos de criar uma função a por P, onde m “fará papel de eixo Ox→ ” e P “fará papel de eixo Oy→. Como nossa função possui a > 0 teremos realmente um ponto máximo.
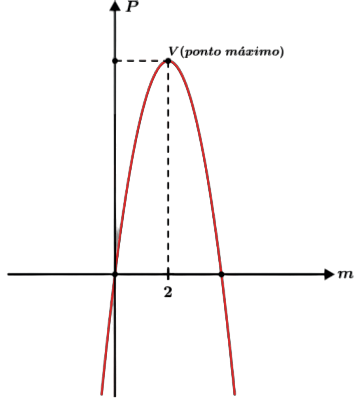
Usando a ideia de x do vértice encontraremos o valor de m que torna o produto P máximo.
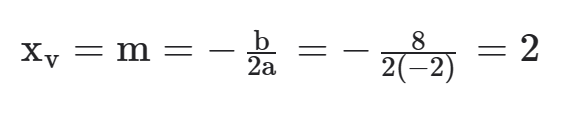
Assim m sendo igual a 2 teremos n = 8 – 2 · 2 = 4.
Assim o produto máximo será P = mn = 2 · 4 = 8.
Note que não calculamos yv pois não era nosso interesse o produto máximo mas sim os valores que tornavam máximo esse produto. Se precisássemos calcular o produto máximo poderíamos ter utilizado
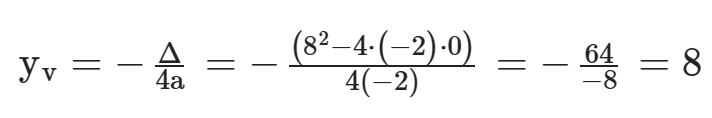
Note que o valor máximo ou mínimo também pode ser encontrando fazendo yv =f (x)v . Assim yv = f(2) = -2(2)2 + 8 · 2 = -2 · 4 + 16 = 8.
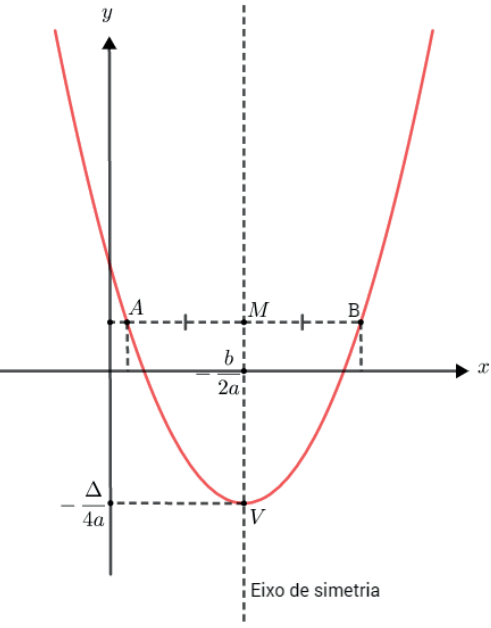
EIXO DE SIMETRIA
O gráfico da função quadrática admite um eixo de simetria perpendicular ao eixo Ox e (paralelo a y) que passa pelo vértice.
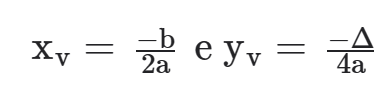
FORMA FATORADA
Se f(x) = ax2 + bx + c possui raízes r1 e r2, podemos fatorar f(x) = a(x – r1)(x – r2).
Exemplo:
Seja f(x) = 6x2 – 5x – 1. As raízes desta função quadrática são 1 e – 1/6. Assim, podemos fatorar tal função como 6(x – 1)(x + 1/6) = (x – 1)(6x + 1).
ESTUDO DO SINAL
Seguem os tipos de gráficos que podemos obter.
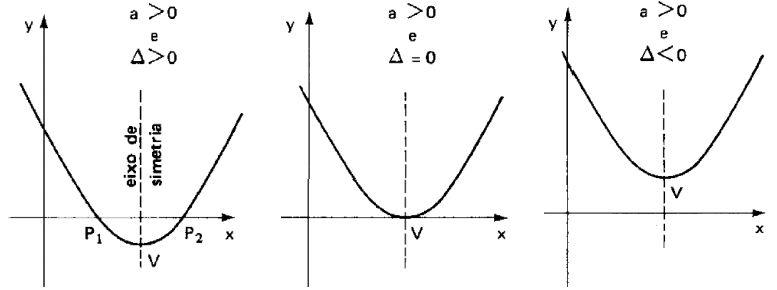
Esses foram os gráficos para a > 0, agora veremos para a < 0.