Vamos ver da mesma maneira um exemplo prático.
Digamos que trabalhamos todas as propriedades necessárias e chegamos a log3x ≥ 3.
Primeiramente vamos a condição de existência de log3x.
log3x ⇒ x > 0
x=27
Então como já sabíamos a igualdade se dará para x=27 mas o que nos foi perguntado foi “quais os valores de x para que log3x seja maior que 3″ e assim podemos pensar o seguinte, a igualdade acontece para x=27, sim, isso nós vimos. Agora vamos pensar o seguinte: x é o resultado de uma potenciação de base de potência 3 onde o logarítmo (resultado) é o expoente.
Assim como nossa base é 3 quanto maior o nosso expoente maior será o resultado e assim quanto maior for o logarítmo maior será x.
log381 > log350 > log330 > log328 > log327 >3
Ou seja, basta termos x ≥ 27 para que a log3x ≥ 3.
Fazendo a intersecção:

Se fizermos a análise para uma base que está entre 0 e 1 teremos o pensamento inverso em relação ao logarítmo e x, assim como nas inequações exponenciais.
Sendo assim teremos também 2 casos

Isso tudo sem esquecermos da condição de existência de um logaritmo.
Vamos ver mais um exemplo.
log2(2x-1) < log26
Como a base do logaritmo é maior que 1, devemos manter a desigualdade.

ProBizu
Repare que as próprias propriedades dos logarítmos nos ajudam.

Podemos ter também inequações onde a substituição será necessária primeiro.
log23x – 3 log3x + 2 >0
Mas antes log3x ⇒ x > 0
Fazendo log3x =m teremos
m2 – 3m + > 0
As raízes por soma e produto temos S=3 e P=2 onde m=1 ou m=2. Assim como temos o a da nossa parábola positivo, teremos.
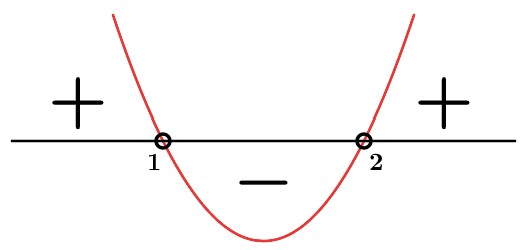
Como não queremos m mas sim x temos que voltar em log3x.
log3x < 1 ⇒ x <31 ⇒ x< 3
Mas como temos também que x > 0 teremos 0 < x < 3
log3x > 2 ⇒ x > 32 ⇒ x > 9
S={x ∈ ℝ ∣ 0 < x < 3 ou x > 9}
Gostou né? Mais um exemplo então.
log2(x2+x-2) ≤2
Da condição de existência temos que x2 + x – 2 > 0 e nossas raízes serão S=-1 e P=-2 onde x=-2 ou x=1.
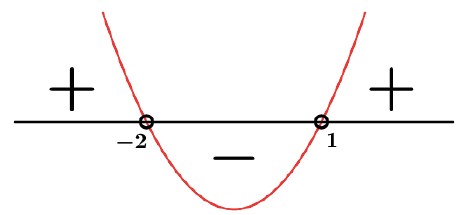
x < -2 ou x > 1
log2(x2 + x – 2) ≤ 2 ⇒ x2 + x – 2 ≤ 22 ⇒ x2 + x – 2 ≤ 4 ⇒ x2 + x – 6 ≤ 0
Encontrando as raízes por soma e produto S=-1 e P=-6 teremos x=-3 ou x=2.
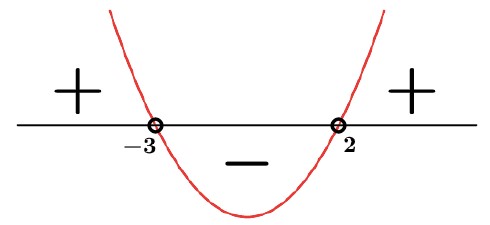
x ≤ – 3 ou x ≥ 2
Agora precisamos fazer a intersecção:

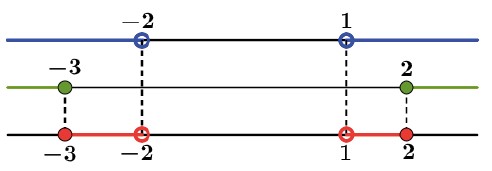
S = { x ∈ ℝ ∣-3 ≤ x < – 2 ou 1 < x ≤ -2}




