Função Logarítmica: Gráficos

BASE MAIOR DO QUE 1:(a>1)

Uma das maneiras de construir o gráfico é achar pontos através da substituição de valores em x, por exemplo. Lembra que falamos que log seria a mesma coisa que expoente?

Veja só a função abaixo por exemplo.

f(x)=log₂x

Temos que y=log₂x⇒x=2^y e podemos pensar o seguinte: para uma potência cuja base é 2 e o expoente é y e x=2^y quanto mais aumentarmos o valor de x (resultado da potência) mas também deve-se se aumentar o expoente y e vice versa.

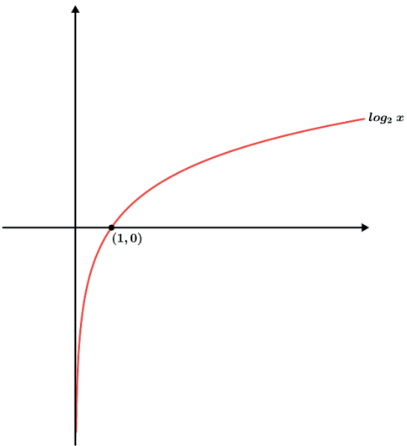
Temos nesse caso o eixo y como uma assíntota pois nunca teremos x=0 em f(x)=log_ax.

Temos como raiz x=1 pois f(x)=0⇒log_ax=0⇒x=a⁰=1.

Uma função f(x)=log_ax com a>1 é uma função crescente.

BASE ENTRE ZERO E 1:(0<a<1)

Agora utilizaremos o mesmo raciocínio anterior. Para exemplificar vamos utilizar a funcão abaixo.

Temos que y=log_¹/² x ⇒ x=(¹/₂)^y e podemos pensar o seguinte: para uma potência cuja base é ¹/₂ e o expoente é y e x=(¹/₂)^y quanto mais aumentarmos o valor de x (resultado da potência) devemos diminuir o expoente y pois temos uma base que está entre 0 e 1 e se quisermos diminuirmos o resultado x devemos aumentar o expoente.

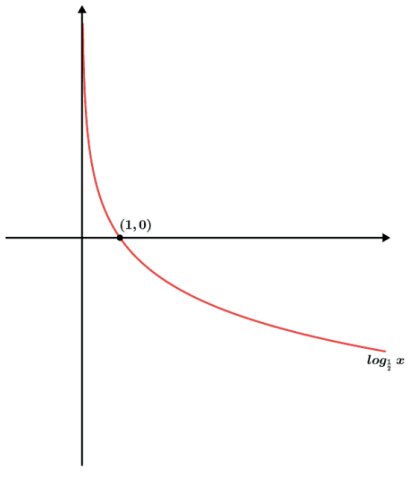
Uma função f(x)=log_ax com 0<a<1 é uma função decrescente.

Nos gráficos acima, podemos perceber algumas propriedades importantes:

– A função logarítmica da forma y=log_ax só existe no 1° e 4° quadrantes. Isso quer dizer que não está definida para x negativo.
– Nos dois casos as funções tendem a encostar no eixo y, mas nunca de fato o tocam. Por conta disso, dizemos que o eixo y é uma assíntota vertical.
– O conjunto imagem da função logarítmica da forma y=log_ax é igual a ℝ.
– A função do tipo y=log_ax também será injetora, pois para diferentes valores do domínio encontraremos diferentes valores no contradomínio.
– Nas funções do tipo y=log_ax, teremos sempre f(1)=0. Portanto, o gráfico da função exponencial sempre interceptará o eixo das abscissas no ponto (1,0).

Mas tudo isso é relativo à função f(x)=log_ax, vimos isso inclusive no módulo de função exponencial. Vamos brincar aqui também?

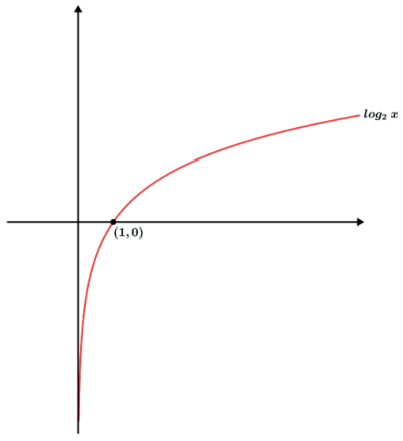
Vamos utilizar como base a função f(x)=log₂x.

• f(x) = log₂x

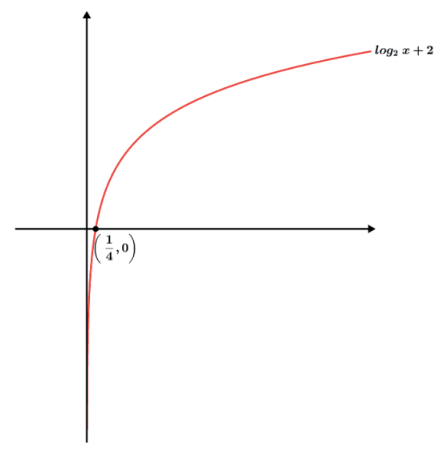
• f(x) = log₂x + 2

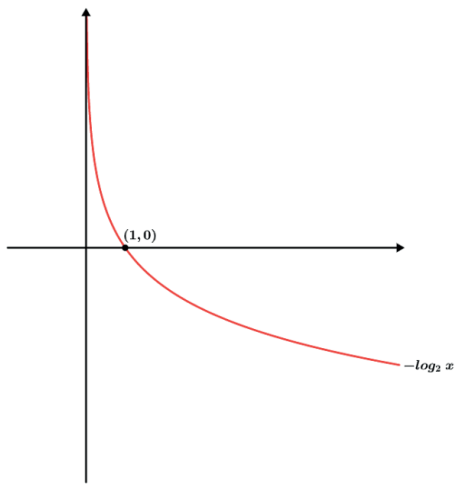
• f(x) = – (log₂x)

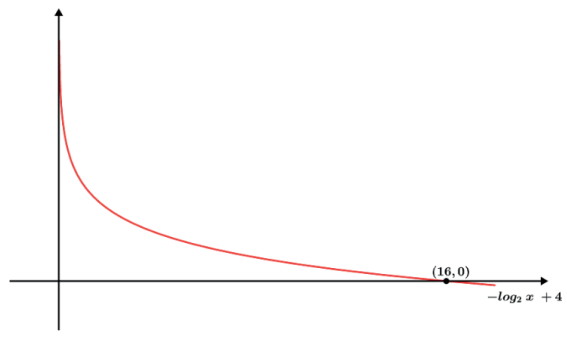
• f(x) = – (log₂x) + 4

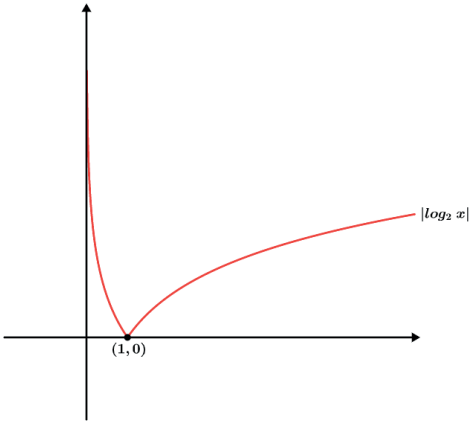
• f(x) = |log₂x|

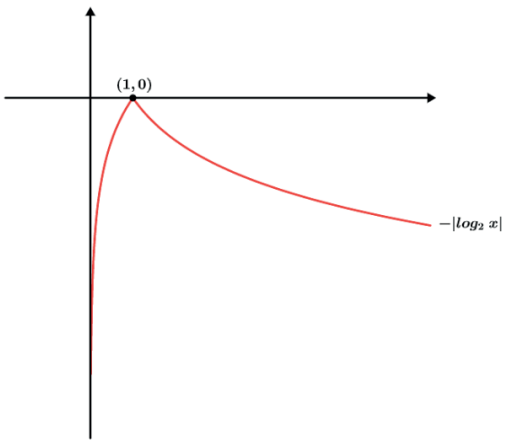
• f(x) = – |log₂x|

• f(x) = – |log₂x| + 2

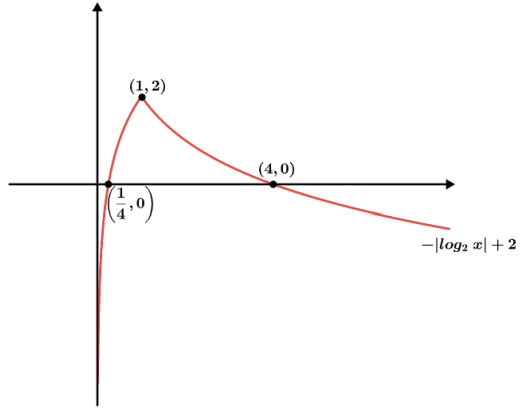
• f(x) = log₂(x + 3)

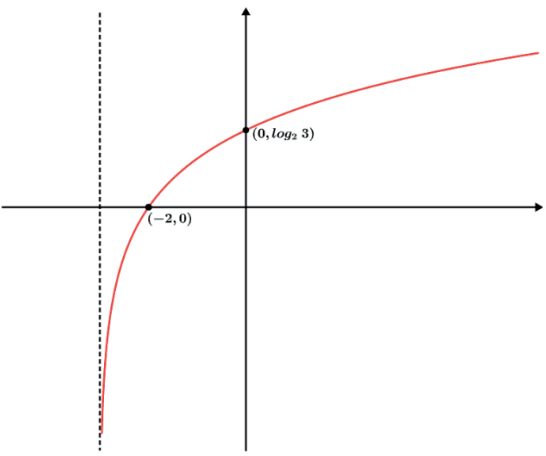
Tivemos mais uma vez oportunidade de reforçar que quando estamos falando de funções, pelo fato das transformações que podem ocorrer, é difícil que tenhamos verdades imutáveis e conseguimos revisar pontos importantes sobre as transformações que as funções podem sofrer.