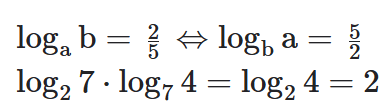DEFINIÇÃO
Em uma base a, onde a>0 e a≠1, o logaritmo de N é αα. O logaritmo de um número é definido como o expoente que é elevado para que potência obtida seja igual a N. Veja, como podemos simbolizar:
logaN= α ⇔ aα=N
Logaritmo é um número real localizado na base que é elevado para obter o logaritmando ou o antilogaritmo (N = antiloga α =aα) , que nesse caso é representado por N, onde “a” é a base e α é o logaritmo.
O logaritmo α existe se:
N>0
a>0
a≠1
O cologaritmo de N na base a é o oposto do logaritmo de N na base a.
cologaN =-logaN
Antilogaritmo de N na base α é definido por
antilogαN= x ⇔ αN=x
Exemplos:
a) log216=4,pois 24=16
b) log525=2, pois 52=25
c) log1/381=-4,pois (1/3)-4=81
d) log41=0, pois 40=1
e) antilog 2=72=49
f) antilog 6=26=64
g) colog24=-log24=-2
h) colog327=-log327=-3
CONSEQUÊNCIA DA DEFINIÇÃO
a) loga1=0, pois a0=1
b) logaa=1, pois a1=a
c) loga(a)α= α, pois aα=aα
d) alogaN=N pois logaN = k, então ak=N e daí alogaN=ak=N
PROPRIEDADES DOS LOGARITMOS
Para: M>0,N>0,a>0 e a≠1.
a) Definimos o logaritmo de um produto através da soma dos logaritmos dos fatores.
Simbolicamente:
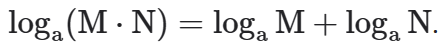
b) Definimos o logaritmo de um quociente através da diferença entre o logaritmo do numerador e do denominador.
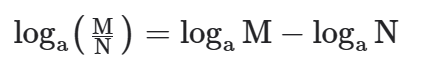
c) Definimos o logaritmo de uma potência através do expoente multiplicado pelo logaritmo da base da potência.
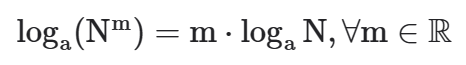
d) Para definirmos o logaritmo de uma raiz basta saber o inverso do índice da raiz multiplicado pelo logaritmo do radicando.
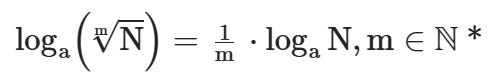
e) Quando a base de um logaritmo estiver elevada a um expoente faremos:
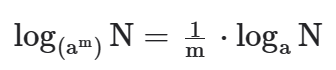
MUDANÇA DE BASE
Para definirmos o logaritmo de um número N(N>0), numa base a a(a>0 e a≠1) basta saber o quociente entre o logaritmo de N e o logaritmo de a, com os dois na base b, onde com b>0 e b≠1.
Para trocar as bases, devemos seguir a regra abaixo:
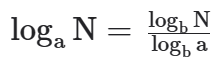
Sejam a,b,c ∈ ℝ+* e a,c ≠ 1, temos: logab =logc b/logc a
Exemplo:
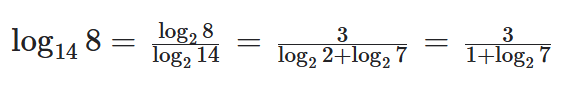
Consequências:
a) logab=1/logb a
b) logca · logab = logcb
c) logab ·logbc · logcd·…·logyz=logaz
Exemplos: