INEQUAÇÕES PRODUTO
Sendo f(x) e g(x) duas funções na variável x, as inequações f(x)·g(x)>0, f(x)·g(x)<0, f(x)·g(x)≥0 e f(x)·g(x)≤0 são denominadas inequações produto.
Exemplo: (x+2)·(2x-1)>0. Um processo prático é fazer o estudo de cada função separadamente. Fazemos o estudo de f(x)=(x+2) e g(x)=(2x+1).
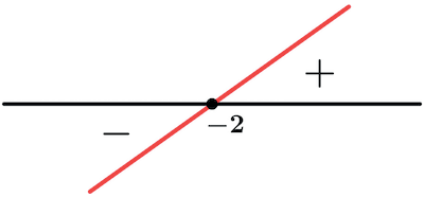
Sinal de f(x) = x+2
Zero da função: f(x) = 0 ⇒ x + 2 = 0 ⇒ x = -2
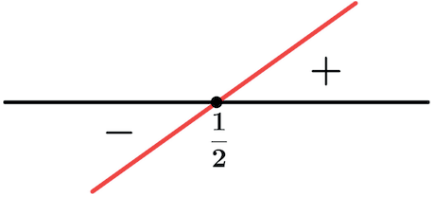
Sinal de g(x) = 2x + 1
Zero da função: g(x)=0⇒2x+1=0⇒x=- 1/2
Agora usamos o auxílio do quadro abaixo onde usamos a regra dos sinais para a multiplicação.
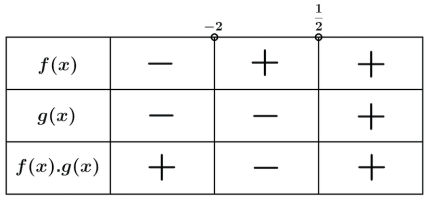
S = {x ∈ ℝ| x < -2 ou x > 1/2}
A inequação f(x)·g(x)≥0 tem como solução a união das soluções de f(x)·g(x)>0 com as soluções de f(x) . g(x) = 0.

Exemplo: resolver a inequação (3x+1)·(2x-5)≥0 em ℝ. Fazemos o estudo de f(x)=(3x+1) e g(x)=(2x-5).
Sinal de f(x)=3 x+1
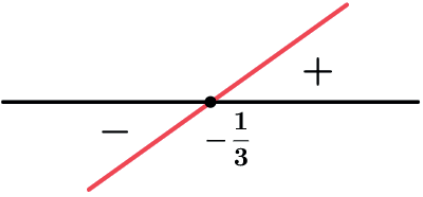
Zero da função: f(x) = 0 ⇒ 3x + 1 = 0 ⇒ x = – 1/3
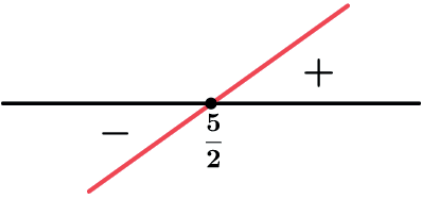
Sinal de g(x)=2 x-5
Zero da função: g(x)=0⇒2x-5=0⇒x=5/2
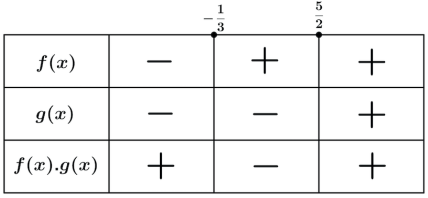
Fazendo o quadro de sinais teremos

Dentre as inequações produto são importantes as inequações do tipo (f(x))n>0, (f(x))n<0, (f(x))n≥0 e (f(x))n≤0. Para resolver essas inequações vamos relembrar as regras de potências:
1) toda potência de base real e expoente ímpar conserva o sinal da base
a2n+1> 0 ⇔ a > 0
a2n+1 = 0 ⇔ a = 0
a2n+1< 0 ⇔ a < 0 (n ∈ ℝ)
2) toda potência de base real e expoente positivo resulta num número não negativo
a2n ≥ 0, ∀a ∈ ℝ, ∀a ∈ ℕ
Assim sendo temos:

Exemplos:

INEQUAÇÕES QUOCIENTE
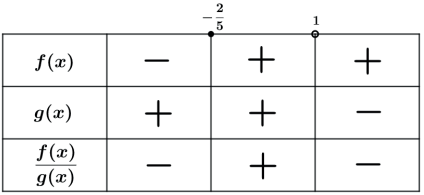
As regras para se resolver as inequações quociente são as mesmas para as inequações produtos, apenas devemos atentar para as restrições de não se poder deixar zerar o denominador da fração pois não existe divisão por zero.

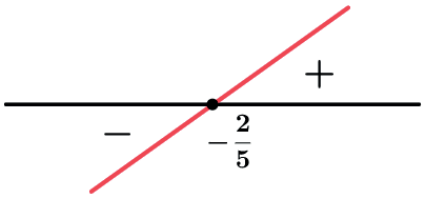
Sinal de g(x)=1-x
Zero da função: g(x) = 0 ⇒ 1 – x = 0 ⇒ x = 1
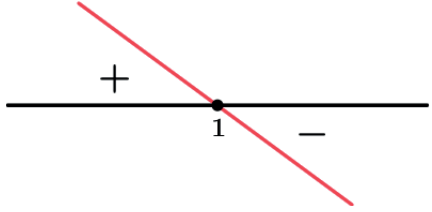
Fazendo o quadro de sinais