Definição: Uma aplicação de f de ℝ em ℝ recebe o nome de função quadrática ou função do segundo grau quando associa a cada elemento x∈ℝ o elemento ax²+bx+c∈ℝ, onde a≠0. Isto é:
f :ℝ→ℝ
x→ax²+bx+c,a≠0
Exemplos:
a) f(x)=x²-3x+2, onde a = 1, b = –3 e c = 2
b) f(x)=2x³+4x-3, onde a = 2, b = 4 e c = -3
c) f(x)=x²-4, onde a = 1, b = 0 e c = –4
d) f(x)=3x²+5x-1, onde a = –3, b = 5 e c = –1
Uma parábola é o conjunto de pontos no plano que são equidistantes de um ponto dado F (foco) e uma reta dada d (diretriz) que não contém F.
CONCAVIDADE
A parábola representativa da função quadrática y=ax²+bx+c pode ter concavidade voltada para “cima” ou para “baixo”.
Se a>0, a concavidade está voltada para cima
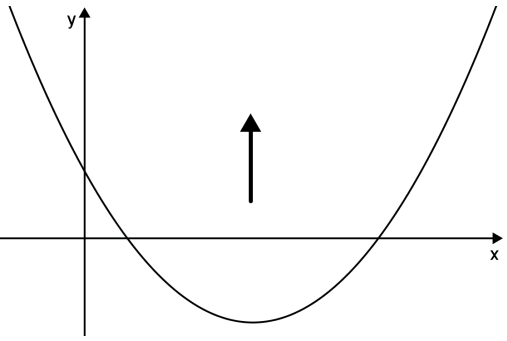
Se a<0, a concavidade está voltada para baixo.
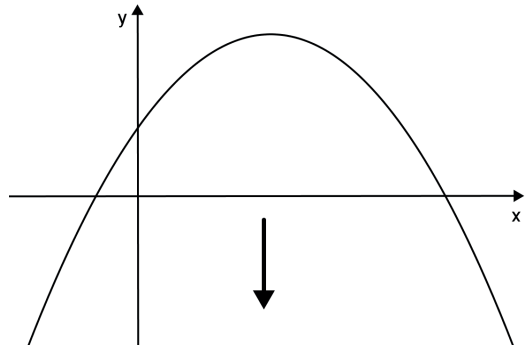
PONTO DE INTERSEÇÃO DA PARÁBOLA COM Oy/y
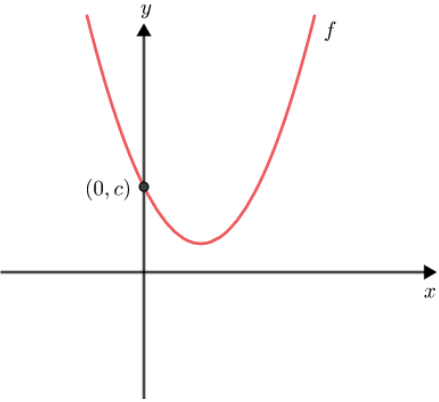
Quando buscamos a intersecção com o eixo Oy→ estamos buscando o ponto da forma (0, f(0)), ou seja, o valor da função f para x=0. Dessa forma temos f(0)=a·0²+0·x+c, sendo f(0)=c, portanto o ponto em que a parábola corta o eixo das ordenadas é o ponto (0.c).
Os zeros ou raízes da função quadrática f(x)=ax²+bx+c são os valores de x reais tais que f(x)=0 e, portanto, as soluções da equação do segundo grau ax²+bx+c.

Discussão – Observe que a existência da raiz da equação do segundo grau ax²+bx+c fica condicionada ao fato de √Δ ∈ R. Assim temos 3 possibilidades distintas.
I. Δ>0, a equação apresentará duas raízes reais e distintas.
II. Δ=0, a equação apresentará duas raízes reais e iguais.
III. Δ<0, a equação não apresentará raízes reais.
Cada sinal do determinante irá determinar uma maneira diferente que a parábola pode ou não interceptar o eixo Ox↔.
SOMA E PRODUTO DAS RAÍZES
Podemos encontrar a soma e o produto das raízes sem antes calcular essas raízes pela fórmula de Bhaskara.

GRÁFICO
Seguem os tipos de gráficos que podemos obter.
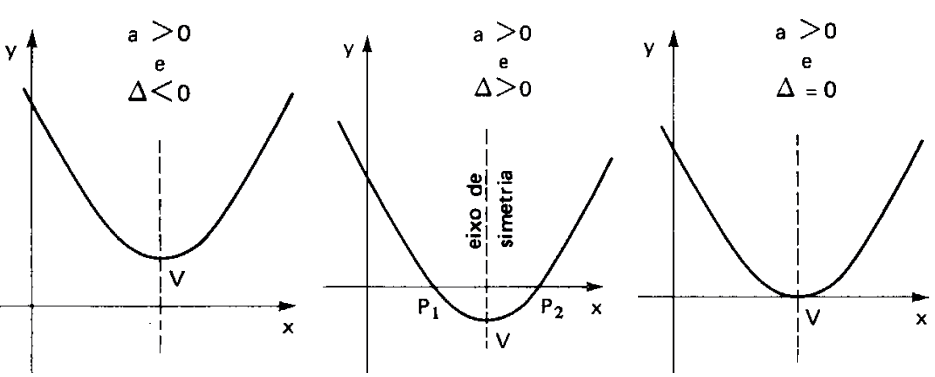
Esses foram os gráficos para a > 0, agora veremos para a < 0.
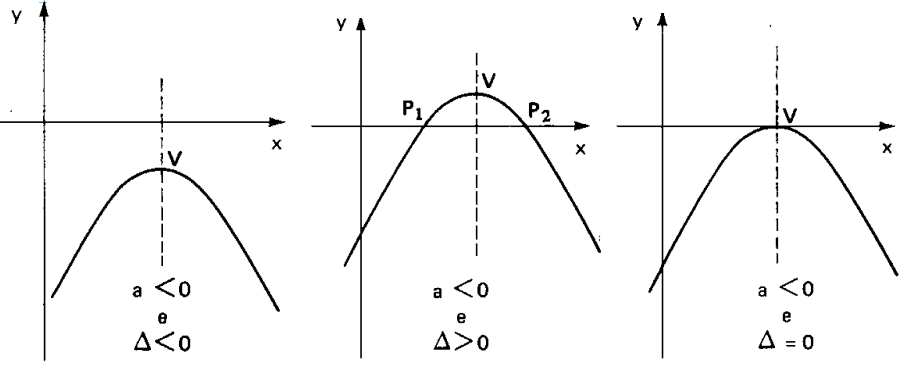
MÁXIMO E MÍNIMO
Vértice da parábola: o ponto V (-b/2a , -Δ/4a) é chamado vértice da parábola representativa da função quadrática.
Máximo e mínimo: O ponto do vértice da parábola é o ponto onde a imagem (ordenada eixo y) e o x são mínimos para a > 0 e são máximos para a<0.
Ponto mínimo (a>0):
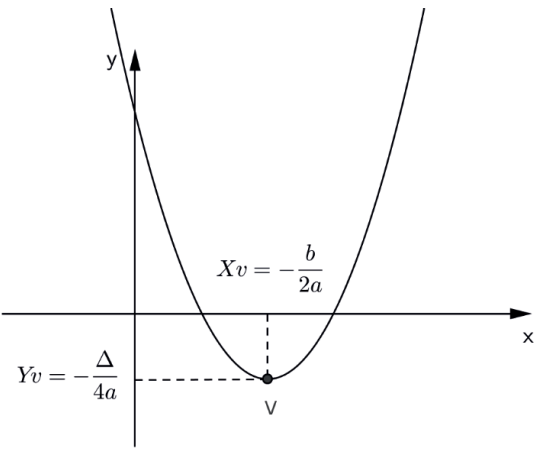
Ponto máximo (a<0):
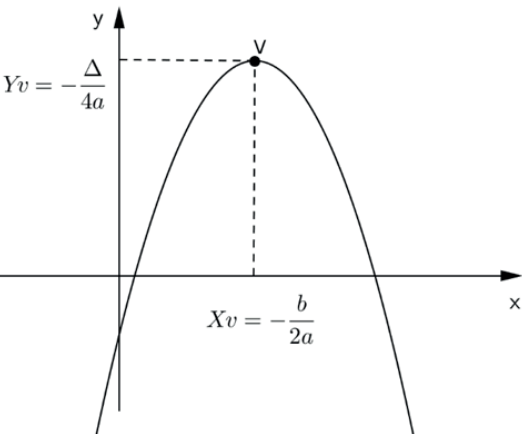
Vamos ver um exemplo.
Sabemos que 2m+n=8, com m e n números reais. Devemos determinar o par m, n que torna o produto m·n máximo.
Veja que podemos isolar n em função de m.
n=8-2 m
Dessa forma vamos chamar o produto de P e assim
P=mn=m(8-2m)=-2m²+8m
Acabamos de criar uma função a por P, onde m “fará papel de eixo Ox↔ “e P “fará papel de eixo Oy↔”. Como nossa função possui a>0 teremos realmente um ponto máximo.
Usando a ideia de x do vértice encontraremos o valor de m que torna o produto P máximo.

Assim m sendo igual a 2 teremos n=8-2·2=4.
Assim o produto máximo será P=mn=2·4=8.
Note que não calculamos yv pois não era nosso interesse o produto máximo mas sim os valores que tornavam máximo esse produto. Se precisássemos calcular o produto máximo poderíamos ter utilizado

Note que o valor máximo ou mínimo também pode ser encontrando fazendo yv= f (xv). Assim yv = f(2)=-2(2²)+8·2=-2·4+16=8.
Eixo de simetria: O gráfico da função quadrática admite um eixo de simetria perpendicular ao eixo dos x e (paralelo a y) que passa pelo vértice.
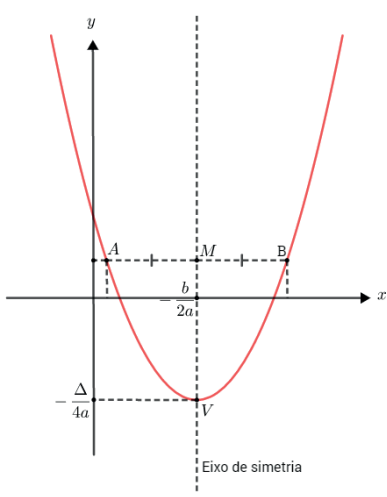

FORMA FATORADA
Se f(x)=ax²+bx+c possui raízes r1 e r2, podemos fatorar f(x)=a (x-r1) (x-r2).
Exemplo: se f(x)=ax²+bx+c. As raízes desta função quadrática são 1 e – 1/6. Assim, podemos fatorar tal função como 6(x-1) (x+1/6) =(x-1) (6x+1).
INEQUAÇÕES DO SEGUNDO GRAU
Se a≠0 as inequações ax²+b x+c>0, ax²+bx+c<0, ax²+bx+c≥0, ax²+bx+c≤0 são denominadas inequações do segundo grau.
Resolver por exemplo a inequação ax²+bx+c>0 é responder a pergunta “existe x ∈ R tal que f(x)=ax²+bx+c seja positiva?”
A resposta a essa pergunta encontra-se na análise do sinal de f(x), que pode, inclusive ser feito pelo gráfico de f(x).
Exemplo: resolver a inequação x²-2x+2>0.
Considerando f(x)=x²-2x+2, temos a=1>0 e Δ=-4<0 então f(x) > 0 para qualquer x ∈ ℝ.
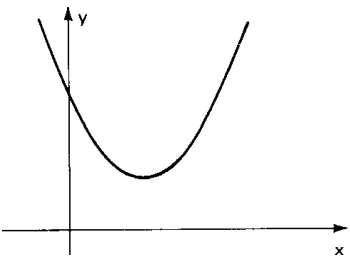
omo a inequação é f(x) > 0 vem S=ℝ.
Resolver a inequação x²-2x+1≤0
Considerando f(x)=x²-2x+1, temos a=1>0,Δ=0, e uma raiz dupla igual a 1 então:

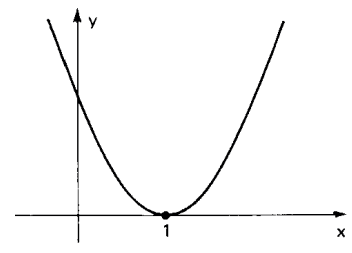
Como a inequação é f(x) ≤ 0, temos S={1}.




