IDENTIFICAÇÃO DOS COEFICIENTES
É importante perceber que os coeficientes não estão ligados a ordem dos elementos, mas sim quem eles acompanham. O coeficiente “a” será sempre aquele que acompanha o termo algébrico x², já o coeficiente “b” será sempre aquele que acompanha o termo x, finalmente o coeficiente “c}” será aquele que não possui termo algébrico, sendo chamado de termo independente. Veja:
3x-x²+1=0⇒a=-1,b=3 e c=1
x-1+2x²=0⇒a=2,b=1 e c =-1
3x²-1=0⇒a=3,b=0 e c=-1
Veja que nem sempre a equação do 2° grau terá todos os termos. Quando possuir todos os termos se chamará equação completa, porém quando “b” ou “c” forem iguais a zero será dita equação incompleta. Vamos ver os métodos de resolução das equações incompletas.
RESOLUÇÃO QUANDO b = 0

Essa é a maneira literal de mostrar a resolução de uma equação do 2° grau quando b=0. De imediato você deve ter percebido que para que haja uma solução real para “x” devemos ter – c/a ≥0, condição essa para que possa haver a radiciação. Vamos verificar exemplos com números.

Neste ultimo exemplo vemos que não há solução real, pois não há como fazer uma radiciação de índice de um número negativo.
ESOLUÇÃO QUANDO c=0

Sempre que c = 0 teremos o “0” como uma das raízes da equação. Lembre-se que a condição para que um produto seja zero é que algum dos fatores seja zero.

RESOLUÇÃO DA EQUAÇÃO COMPLETA (FÓRMULA DE BASKARA)
Para resolução da equação completa usamos uma fórmula pronta, chamada fórmula de bhaskara, onde basta apenas substituir os coeficientes da equação na fórmula.
A fórmula é a seguinte:

Como nessa fórmula há uma raiz de grau 2 (raiz quadrada), vão existir valores de a, b e c que farão com que b² – 4ac seja negativo. Dessa forma nomeamos b²- 4ac de determinante, ou discriminante, para sabermos antecipadamente se haverá solução para a equação do 2° grau ou não. Assim:
Δ>0→2 raízes reais e distintas
Δ=0→2 raízes reais e iguais
Δ<0→ não há raízes reais
Fazendo com que a equação possa ser escrita dessa forma x=-b±√Δ/2a , onde Δ=b²-4ac. Dessa forma podemos ver alguns exemplos:

Exemplo 1: x²-4x+3=0

fazendo o determinante separado ou não teremos logicamente o mesmo valor. As vantagem de fazer o determinante separado é poder ver antecipadamente se a equação irá admitir raízes reais ou não. Neste nosso exemplo vemos que Δ=4>0 e dessa forma teremos 2 raízes reais e distintas.

Exemplo 2: x²-8x+16=0
a=1, b=-8 e c=16 ⇒ Δ=(-8)²-4·1·16=64-64=0
Então já sabemos que esta equação admite 2 raízes reais, porém iguais. Assim:

Exemplo 3: 2x²-3x+5=0
a=2,b=-3 e c=5⇒Δ=(-3)²-4·2·5=9-40=-31⇒Δ<0
Dessa forma a equação 2x²-3x+5=0 não admitirá raízes dentro do conjunto dos números reais, assim seu conjunto solução é vazio.
Ǝ̶x ∈ ℝ/2x² – 3x + 5 = 0 ⇒ S = Ø
Exemplo 4: achar as raízes de x²-5x+6=0.
Δ=b²-4ac=(-5)²-4(1)(6)=1.
A equação tem duas raízes reais distintas x1=5+√1/2 = 3 e x2 =5-√1/2=2.
x¹=3,x²=2
Exemplo 5: achar as raízes de x²-6x+9=0.
Δ=(-6)²-4(1)(9)=0.
A equação tem uma raiz dupla x1 e x2= 6/2 =3.
x¹ e x²=3
Exemplo 6: resolver 2x²+x+8=0.
(6)2-4(2)(8)=-63.
Como Δ<0, a equação não possui raízes reais.
SOMA E PRODUTO DAS RAÍZES
Da fórmula de Baskara podemos perceber que as raízes são x1=-b+√Δ/2a e x2=-b-√Δ/2a, assim podemos calcular a soma e o produto delas.

Daí temos que a soma das raízes de uma equação do 2° grau é sempre igual a – b/a e o produto é sempre igual a c/a.
Vamos ver alguns exemplos.
1º. Sabendo que as raízes da equação 2x²-5x+3=0 são m e n, calcule o que se pede em cada opção.
a) m + n
O que é pedido pela questão e a soma das raízes, dessa forma m+n= s =- b/a=- -5/2= 5/2
b) m·n
O que é pedido é o produto das raízes, m·n=P = c/a = 3/2
c) m·n²
O que é pedido é a soma das raízes elevada ao quadrado, (m+n)²=(S)²=(5/2)²= 25/4.
d) m²+n²
O que é pedido pela questão é a soma dos quadrados das raízes, precisaremos utilizar o que aprendemos de produtos notáveis.
(m+n)² = m² + 2mn +n2 ⇒ m² + n² + 2mn=(m+n)² ⇒
⇒ m²+n² = (m+n)² -2mn
Assim percebemos que m²+n² pode ser escrito somente em função da soma S e do produto P das raízes.

FUNÇÕES SIMÉTRICAS DAS RAÍZES

DEMONSTRAÇÃO DA FÓRMULA DE BÁSKARA E A RESOLUÇÃO GEOMÉTRICA
A fórmula de Báskara pode ser demonstrada através do método conhecido por completar quadrados.
ax²+bx+c=0
Primeiramente iremos dividir toda a equação pelo coeficiente a.

Agora vamos fazer com que o lado esquerdo da igualdade seja um quadrado perfeito completando os quadrados.
x²+bx/a para ser um quadrado perfeito precisaremos somar o quadrado do 2º termo onde teremos que. Sendo x o 1º termo teremos que o 2º termo será a metade de b/a, logo o 2º é b/2a.
Vamos somar nos 2 lados da equação o quadrado de b/2a.

O mulçumano al-Khowarizmi estudou a Álgebra geométrica de Euclides e resolveu uma equação do 2º grau através da mesma.
Vamos resolver a equação do 2º grau x²+6x-27=0.
Vamos primeiramente fazer x²+6x=27.
Vamos imaginar um quadrado de lado x.
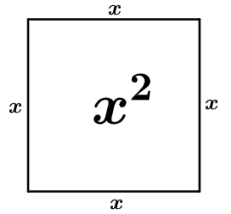
Logo a área do quadrado é x².
Agora vamos imaginar um retângulo de área 6x.
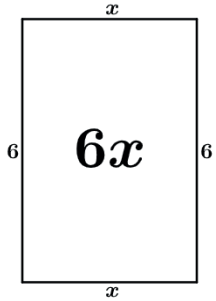
Vamos dividir esse retângulo em 4 retângulos iguais sendo uma das dimensões igual a x.
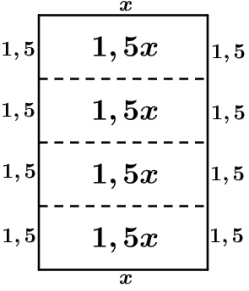
Vamos colocar cada retângulo em cada um dos lados do quadrado.
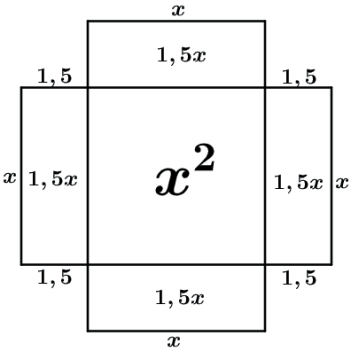
Temos que a área total da figura acima é x²+6x e temos da nossa equação que x²+6x=27. Vamos agora completar um quadrado grande completando 4 quadrados pequenos de lado 1,5 por 1,5.
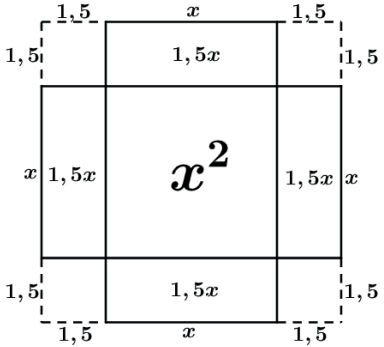
A área de cada quadrado pequeno é 1,5 x 1,5 = 2,25 fazendo com que a área que nós tínhamos (27) tenha 4 quadrados de área 2,25 adicionados totalizando 27+4⋅2,25=36.
Um quadrado de área 36 tem um lado de medida igual a 6.
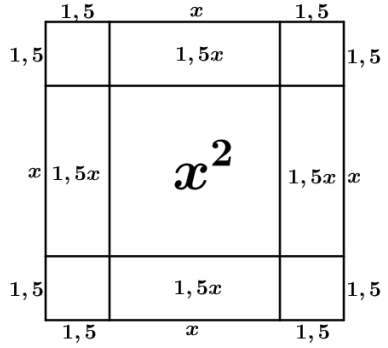
endo o nosso quadrado de lado 6 teremos quex+1,5+1,5=6⇒x=3.
Exemplo 1: sendo x1 e x2 as raízes da equação x²–x–12=0, o resultado da soma x1+x2 é:
a) 1
b) 3
c) 4
d) 7
e) 12
Resolução: A
Utilizando a técnica de soma e produto, temos que a soma das raízes deve ser

Exemplo 2: problemas que recaem numa equação do segundo grau já apareciam em textos escritos pelos babilônios, nas tábuas cuneiformes. Observe a equação x²–12x+p=0. Determine o valor de p, para que uma das raízes seja o dobro da outra.
a) 25
b) 30
c) 32
d) 35
Resolução: C
Pelas Relações de soma e produto, pode-se escrever:





