Se f é uma função de A em B, bijetora, a relação inversa de f é uma função de B em A, chamada função inversa de f e denotada por f-1 e também é bijetora.
A definição acima resulta nas seguintes expressões:
Exemplo:
(x, y) ∈ f ⇔ (y, x) ∈ f-1
f(x) = y ⇔ f-1(y) = x
A função inversa é composta pelos pares ordenados obtidos pela inversão da ordem dos elementos dos pares ordenados da função original.
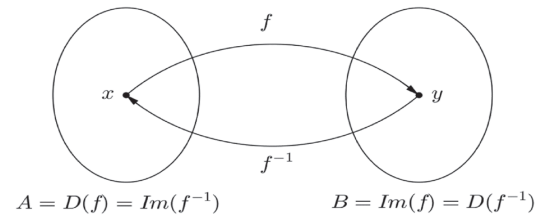
Assim, se a função f : A → B associa cada elemento x ∈ A a um elemento correspondente y ∈ B, a função f-1, inversa de f, associa a cada elemento y ∈ B, o elemento correspondente x ∈ A.
Exemplo: seja a função bijetora f(x) = 2x + 1, encontre o valor de f-1(7).
Observe que para essa questão não é necessário obter a expressão de f-1, apenas usar a definição de relação inversa.
f-1(7) = x ⇔ f(x) = 7
Vamos usar a expressão de f(x) para encontrar o valor de x tal que f(x)=7:
f(x) = 2x + 1 = 7 ⇔ x = 3
Daí se conclui que: f-1(7) = 3.
ProBizu: uma função só possui inversa se ela for bijetora.
No caso de funções que não são bijetoras, a relação inversa está definida, mas ela não é uma função, pois pode haver elementos no conjunto de partida que não estejam relacionados a ninguém ou a mais de um elemento no conjunto de chegada.
O domínio da função inversa é a imagem da função original e a imagem da função inversa é o domínio da função original.
D(f-1) = Im(f) e Im(f-1) = D(f)
Esses conceitos podem ser observados nos diagramas de flecha seguintes:
ProBizu: para encontrar a imagem de uma função bijetora, basta encontrar o domínio da sua função inversa.
Exemplo: encontre a imagem de:

Vamos começar encontrando a inversa de f.

Substituindo-se a variável y por x, temos:

Observe agora que o domínio de f-1 é Df-1 = ℝ*, pois o denominador x deve ser não nulo.
Mas sabemos que a imagem de uma função inversível é igual ao domínio da sua função inversa, então a imagem de f é Imf = Df+1 = ℝ*.
A função inversa da função inversa é a função original.
(f-1)-1=f
O resultado da aplicação da função composta de f-1 com f sobre um elemento x ∈ Df é o próprio x, ou seja, a composição da função inversa com a função original é a função identidade.
(f-1 ∘ f)(x) = f-1(f(x)) = x, ∀x ∈ Df
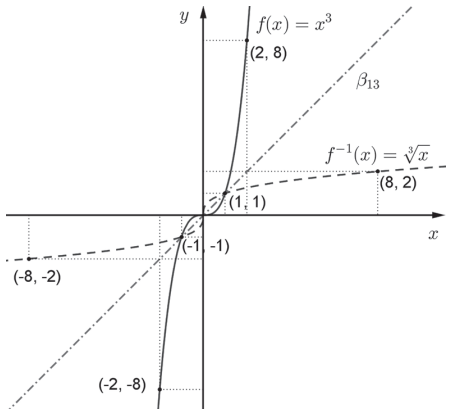
Como (x, y) ∈ f ⇔ (y, x) ∈ f-1, os gráficos de f e f-1 são simétricos em relação à bissetriz dos quadrantes ímpares (β13), como pode ser visto no exemplo abaixo:
OBTENÇÃO DA FUNÇÃO INVERSA
Diversos exercícios solicitam que se encontre a expressão da função inversa, identificando o seu domínio. A seguir vamos apresentar duas maneiras de fazer isso.
1º MÉTODO:
Na expressão y = f(x), efetuamos as operações algébricas necessárias a fim de obter uma expressão de x em função de y. Essa é a expressão da função inversa, ou seja, x = f-1(y).
Ao final, pode ser efetuada a substituição da variável x por y, vice-versa, resultando a expressão y = f-1(x), onde x ∈ Df+1.
Exemplo: obtenha a expressão da função inversa da função bijetora f : ℝ→ℝ, definida por y = 2 x – 4.
2º MÉTODO:
Sabemos que f(f-1(x)) = x. Vamos, inicialmente, obter a expressão de f(f-1(x)), substituindo x por f-1(x) na expressão de f(x). Na expressão encontrada, efetuamos as operações algébricas necessárias para isolar f-1(x).
Exemplo: obtenha a expressão da função inversa da função bijetora f : ℝ → ℝ, definido por y = 2x – 4.

Muitas vezes, para obter a expressão da função inversa, é necessário identificar, dentre as possíveis expressões encontradas, aquela que corresponde ao domínio adotado para a função original.




