Função Exponencial: Gráfico

DEFINIÇÃO

Sendo a>0, a≠1, um número real, definimos a função f:ℝ→ℝ+* como sendo f(x)=ax. Tal função é dita função exponencial de base a.

GRÁFICO

Como vimos, a base da função exponencial precisa estar presente no intervalo a>0 e a≠1.

Vamos dividir e analisar separadamente duas situações para a base.

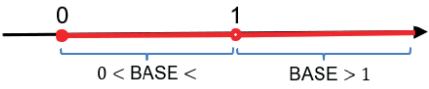
FUNÇÃO CRESCENTE (BASE > 1)

Exemplo: f(x)=(2)x

Para montar o gráfico da função y=2x, podemos descobrir pontos substituindo valores de x e realizando as contas.

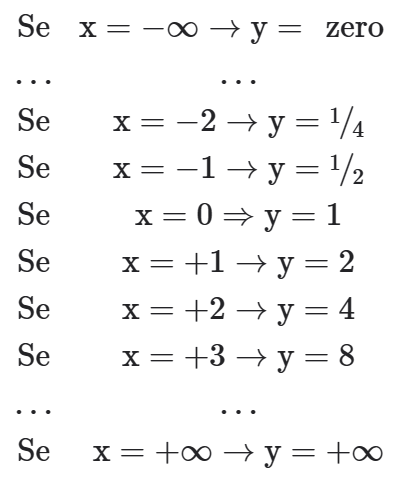
Montando o gráfico a partir dos pontos acima, temos:

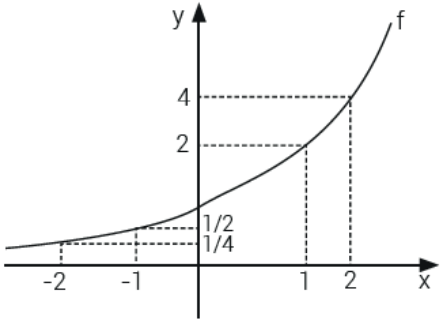
FUNÇÃO DECRESCENTE (0 < BASE < 1) 

Exemplo: f(x)=(1/2)^x

Para montar o gráfico da função y=^2x, podemos descobrir pontos substituindo valores de x e realizando as contas.

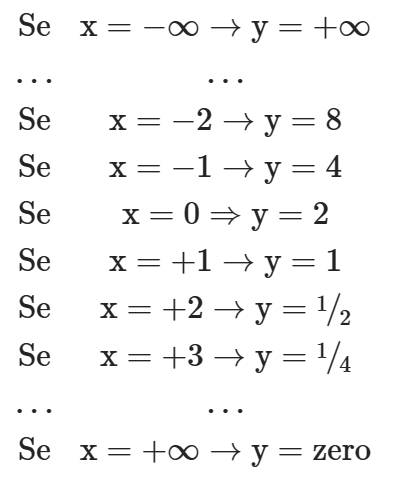
Montando o gráfico a partir dos pontos acima, temos:

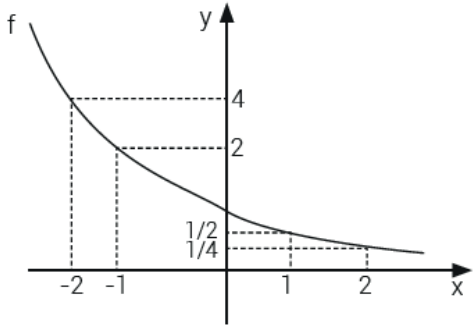
Nos gráficos acima, podemos perceber algumas propriedades importantes:

– A função exponencial da forma y=a^x só existe nos dois primeiros quadrantes. Isso ocorre pois não importa o valor de x,y será sempre positivo.

– Nos dois casos as funções tendem a encostar no eixo x, mas nunca de fato o tocam. Por conta disso, dizemos que o eixo x é uma assíntota horizontal.

– O conjunto imagem da função exponencial y=a^x é igual aℝ₊^*.

– A função do tipo y=a^x também será injetora, pois para diferentes valores do domínio encontraremos diferentes valores no contradomínio.

– Nas funções do tipo y=a^x, teremos sempre f(0)=1. Portanto, o gráfico da função exponencial sempre interceptará o eixo das abscissas no ponto (0,1).

Mas tudo isso é relativo à função f(x)=a^x, como vimos no estudo das funções há diversas operações que que podem ser aplicadas a a^x fazendo com que seu gráfico se modifique, vamos ver alguns exemplos.

Vamos utilizar como base a função f(x) = 2^x

• f(x) = 2^x

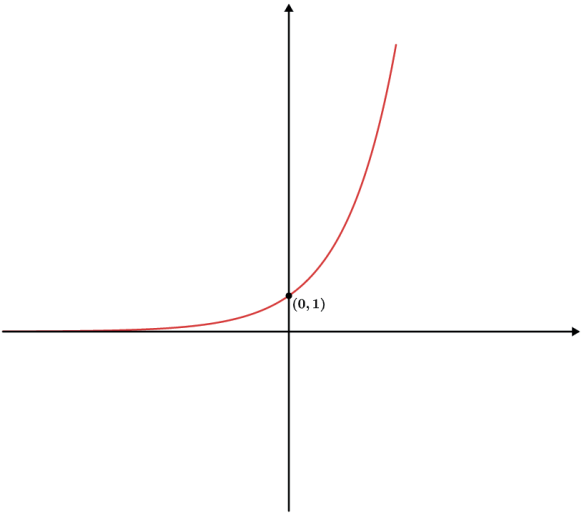
• f(x) = 2^x + 2

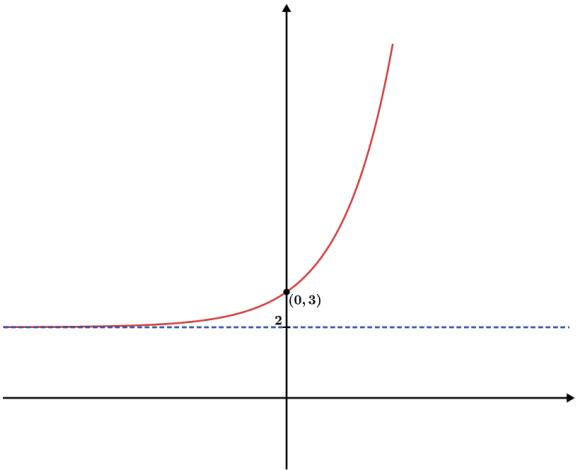
• f(x) = – (2^x)

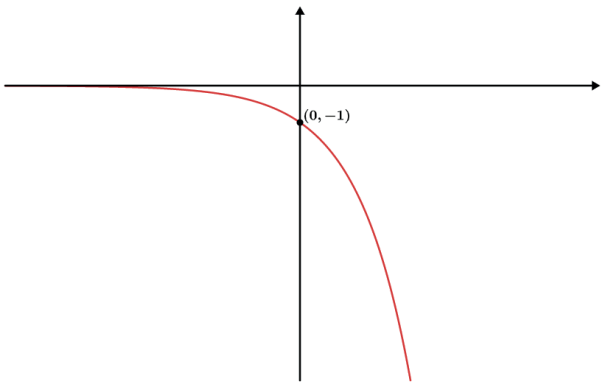
• f(x) = -(2^x) + 4

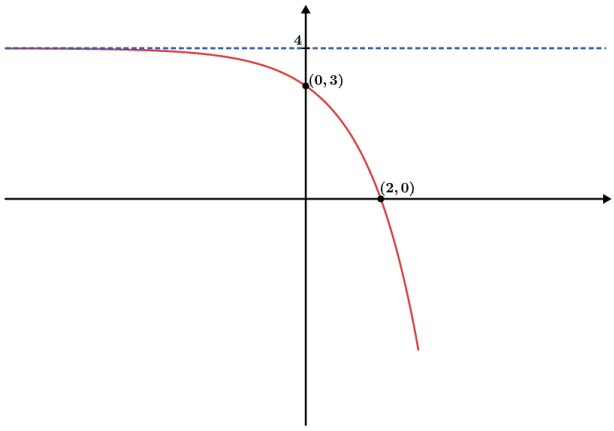
• f(x) = | -(2^x) + 4|

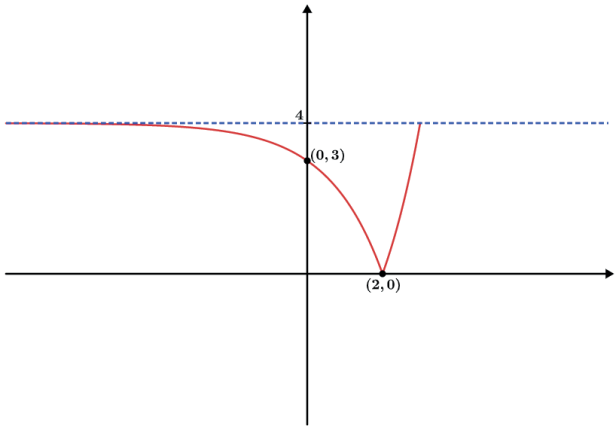
• f(x) = -| -(2^x) + 4|

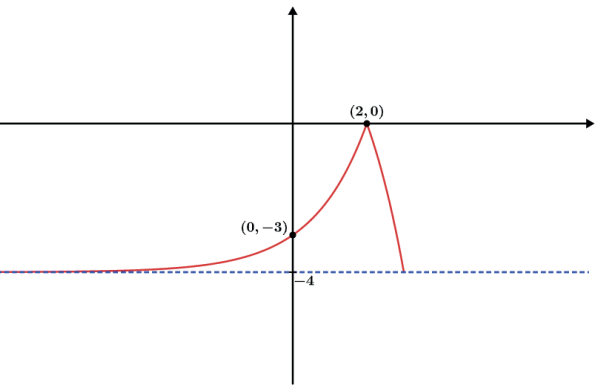
• f(x) = -| -(2^x) + 4|+2

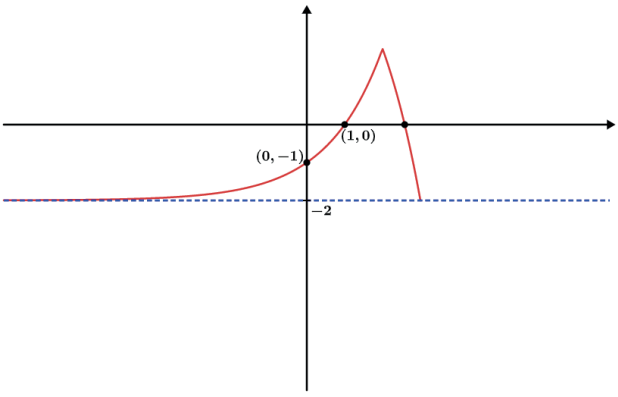
Conseguimos muitas coisas interessantes.

1. Reforçar que quando estamos falando de funções, pelo fato das transformações que podem ocorrer, é difícil que tenhamos verdades imutáveis.

2. Conseguimos aqui revisar pontos importantes sobre as transformações que as funções podem sofrer inclusive no que diz respeito as funções modulares.