Função Exponencial: Definição e propriedades

A potência de expoente n, n natural e n>1, do número a, representa-se por aⁿ, é o produto de n fatores iguais a “a”.

Representa-se por a^m × aⁿ =a^m+n onde a é denominado base e n é denominado expoente.

Quando n=2, lê-se a² como “a ao quadrado” e quando n=3, a³ lê-se como “a ao cubo”.

Exemplos:

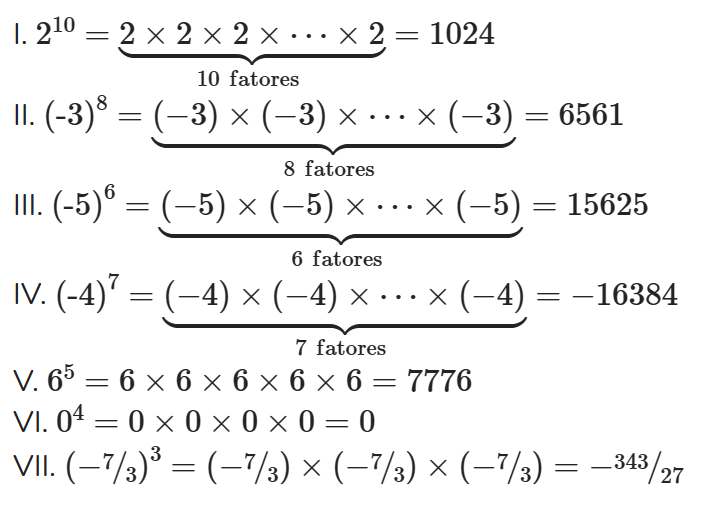
Estende-se a definição de potência pondo-se

(I) a¹=a, para todo a real e a⁰=1, para todo a real diferente de zero.
(II) Dado um número real, não nulo, e um número natural n define-se a potência a^-n pela relação:

Exemplos:

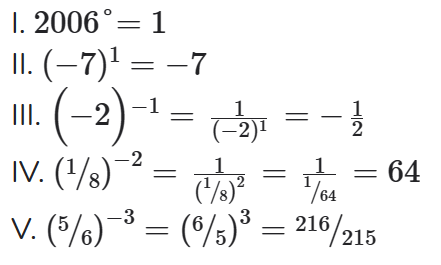
Observação:

Das definições anteriores decorre que a base a das potências pode ser um número real positivo, negativo ou nulo e, com base nisto, podemos fazer as seguintes observações:

(1) toda potência de expoente par é positiva;
(2) toda potência de expoente ímpar tem sempre o sinal da base;
(3) toda potência de 0 com expoente positivo é igual a zero. Não se definem 0° nem 0ⁿ com n negativo;
(4) as potências de (-1) são iguais +1 ou (-1) conforme o expoente seja par ou ímpar respectivamente.

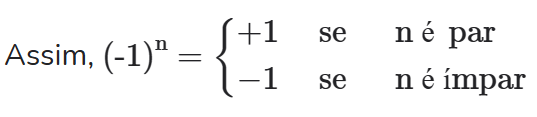
OPERAÇÕES COM POTÊNCIAS

(I) Para multiplicar potências de mesma base, basta conservar a base e somar os expoentes. Assim,

a^m × aⁿ = a^m+n

(II) Para dividir potências de mesma base, conserva-se a base e subtraem-se os expoentes. Assim,

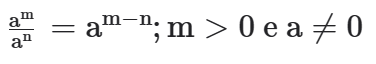
(III) Para calcular uma potência de uma potência, conserva-se a base e multiplicam-se os expoentes. Assim,

(a^m)ⁿ=a^m×n=(aⁿ)^m

Não devemos confundir a^np com (aⁿ)^p pois a primeira é uma potência cujo expoente é uma potência enquanto que a segunda é uma potência de uma potência.

Definição

Potências semelhantes são aquelas que possuem o mesmo expoente.

(IV) Para multiplicar potências semelhantes conserva-se o expoente e multiplicam-se as bases. Assim,

aⁿ×bⁿ=(a×b)ⁿ

(V) Para dividir potências semelhantes conserva-se o expoente e dividem-se as bases. Assim,

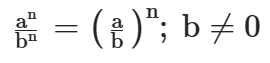
RADICIAÇÃO

Definição: O número real b, é a raiz de índice n (raiz enésima), sendo n um número natural, do número real a se, e somente se ⁿ√a=b ⇔ bⁿ=a onde, se n é par, devemos ter a≥0 e b≥0.

Quando n=2 escreve-se √a ao invés de ²√a para representar a raiz quadrada positiva de a.

Quando n=3, ³√a é chamada de raiz cúbica de a.

O número real a é chamado radicando e ⁿ√a é chamado radical de índice n.

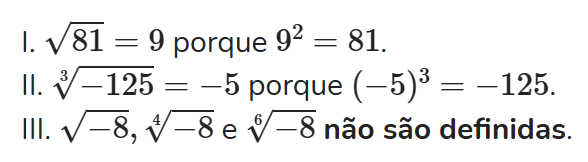
Consequência da definição: decorre imediatamente da definição da raiz enésima de a que (ⁿ√a)ⁿ= a. Assim, (³√6)³=6.

Observação: 

(I) Para todo natural n não nulo, ⁿ√0=0 e ⁿ√1=1.
(II) Para todo natural n e quaisquer reais não nulos a e b tem se que a = b ⇔ ⁿ√a = ⁿ√b e a < b ⇔ ⁿ√a < ⁿ√b. Em particular, a < 1 ⇔ a < ⁿ√a < 1 e a >1⇔1< ⁿ√a <a.

LEI DOS RADICAIS

Para todos os naturais não nulos n e p e todos os reais não nulos a e b valem as seguintes fórmulas.

(l) Para multiplicar raízes de mesmo índice conserva-se o índice e multiplicam-se os radicandos.

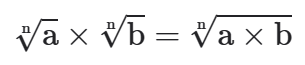
(II) Para dividir raízes de mesmo índice conserva-se o índice e dividem-se os radicandos.

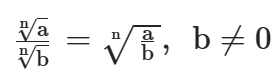
(III) Para elevar uma raiz a um expoente eleva-se o radicando ao expoente e conserva-se o índice da raiz.

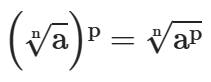
(IV) Para se extrair a raiz de uma raiz conserva-se o radicando e multiplicam-se os índices.

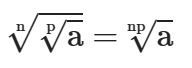
(V) Um radical não se altera quando multiplicamos o seu índice e o expoente do radical por um mesmo natural diferente de zero.

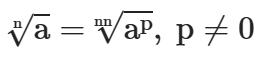
(I) Quando a > 0 e n é par, a notação ⁿ√a representa também a raiz n-ésima positiva de a (a negativa é representada por –ⁿ√a).

Em particular,

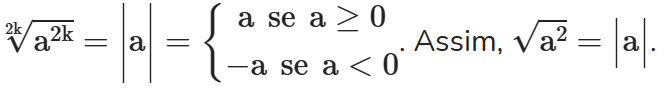
(II) Quando a<0 e n for ímpar as leis das raízes podem ser aplicadas para –ⁿ√|a| (ou –ⁿ√-a ) mas não para ⁿ√a. Assim, por exemplo para reduzirmos ³√-2 a um radical de índice 6 devemos fazer ³√-2= ³√-2= –⁶√2² =- ⁶√4 e não -³√2=⁶√(-2)² = ⁶√4.

POTÊNCIA DE EXPOENTE RACIONAL

Para dar significado às potências de expoentes fracionárias precisamos do uso de radicais. A razão para isto, é que precisamos definir a^¹/_n de modo que ela seja consistente com as leis dos expoentes isto é, devemos ter:

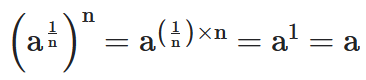
Portanto definiremos,

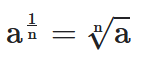
Observemos que se n é par é necessário que a≥0.

Finalmente, definiremos a potência para todo expoente racional irredutível ^m/_n onde m e n são inteiros e n>0.

Se ⁿ√a existe como um número real (e este será o caso para todo número real a se n for ímpar e para a≥0 se n for par), definimos a ^m_/n =(ⁿ√a)^m ou equivalentemente a ^m_/n= ⁿ√a^m.