Vimos que o eixo paralelo ao eixo Ox com a mesma orientação que este e passando pelo ponto B é denominado eixo das cotangentes.
Vimos também que, se um ângulo θ tal que θ ≠ k · π, k ∈ ℤ, tem imagem no ciclo trigonométrico P, então a cotangente de θ é a medida algébrica do segmento B̲P̲2, onde P2 é a interseção da reta O̲P̲ com o eixo das cotangentes.
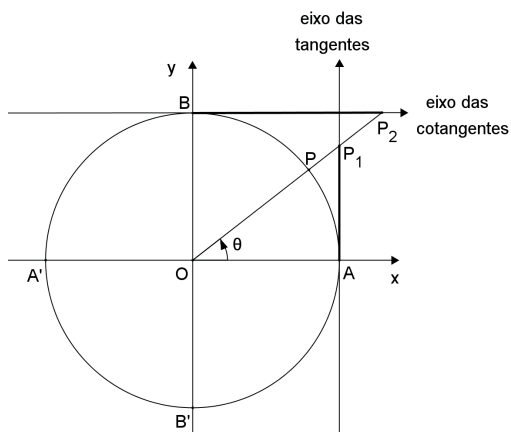
cotg θ = B̲P̲2
A função cotangente é a função de Dcotg em ℝ definida por f(x)=cotg x.
O domínio da função cotangente é Dcotg = {x ∈ ℝ ∣ x ≠ kπ, k ∈ ℤ} e a imagem 1mcotg = ℝ.
A função cotangente é periódica de período π.




