PAR ORDENADO E PLANO CARTESIANO
O conceito de par ordenado, denotado por (a, b), é um conceito primitivo sendo um conjunto de dois elementos ordenados.
Dois pares ordenados são iguais se, e somente se, as suas duas coordenadas são iguais.
(a, b)= (c, d) ⇔ a = c ∧ b = d
Os pares ordenados podem ser representados graficamente em um plano cartesiano ortogonal, onde o primeiro elemento do par ordenado é representado no eixo horizontal Ox (eixo das abscissas) e o segundo elemento do par ordenado é representado no eixo vertical Oy (eixo das ordenadas). Isso pode ser observado na figura a seguir:
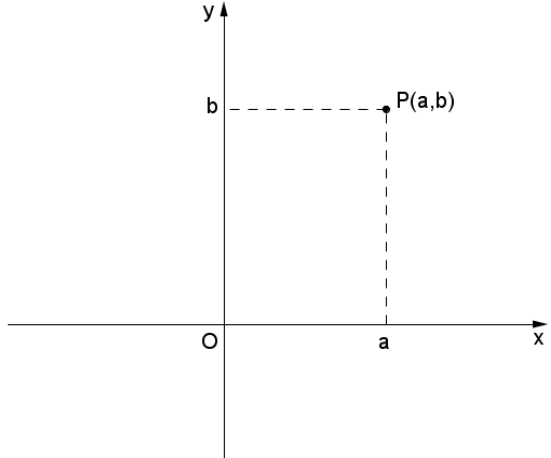
Assim, dizemos que o par ordenado (a,b) possui abscissa a e ordenada b.
PRODUTO CARTESIANO
O produto cartesiano de dois conjuntos A e B é o conjunto de todos os pares ordenados que têm o primeiro termo em A e o segundo termo em B.
A × B = {(x, y) ∣x ∈ A ∧ y ∈ B}
Se um dos conjuntos for vazio, o produto cartesiano é vazio, ou seja, ∅ × B = A × ∅ = ∅ × ∅ = ∅.
O produto cartesiano não é comutativo, assim A × B ≠ B × A, quando A ≠ B.
O produto cartesiano de um conjunto por ele mesmo é denotado por A2 = A × A.
No caso de dois conjuntos finitos, o número de elementos do produto cartesiano pode ser obtido multiplicando a quantidade de elementos de cada um deles.
n(A × B) = n(A) · n(B)
Exemplos:
A = {0,2} e B={1,3,5}
A × B = {(0,1);(0,3);(0,5);(2,1);(2,3);(2,5)}
B × A = {(1,0);(1,2);(3,0);(3,2);(5,0);(5,2)}
n(A × B) = n(B × A) = 2 · 3 = 6
É possível representar o produto cartesiano graficamente através de um diagrama de flechas.
Sendo A = {1,2,3} e B = {1,2,3,4}, então A × B = (1,1);(1,2);(1,3);(1,4);(2,1); (2,2); (2,3); (2,4); (3,1);(3,2);(3,3); (3,4) terá a representação abaixo.
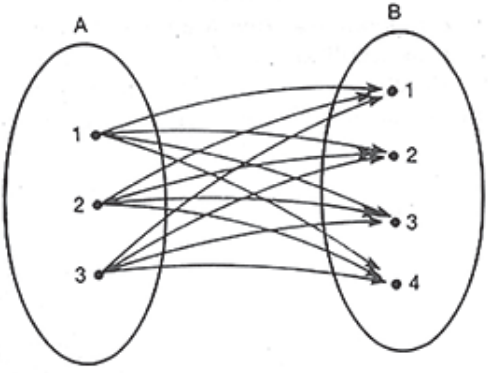
D(R) ⊂ A e Im(R) ⊂ B
O produto cartesiano pode ser representado graficamente no plano cartesiano ortogonal, através da representação dos pares ordenados que o compõem.
A representação gráfica é útil também para apresentar o resultado do produto cartesiano entre intervalos reais.
Exemplo 1: A = {1,2,3} e B = {1,2}
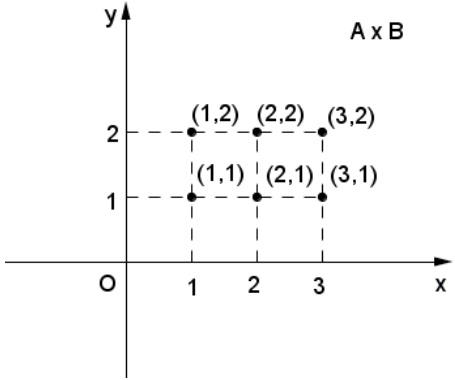
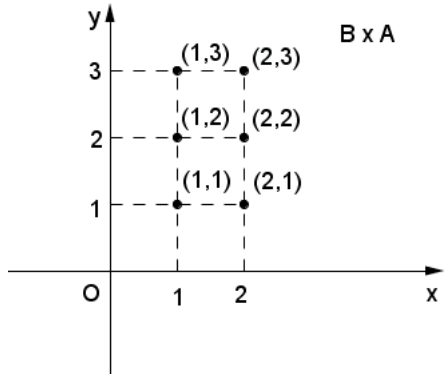
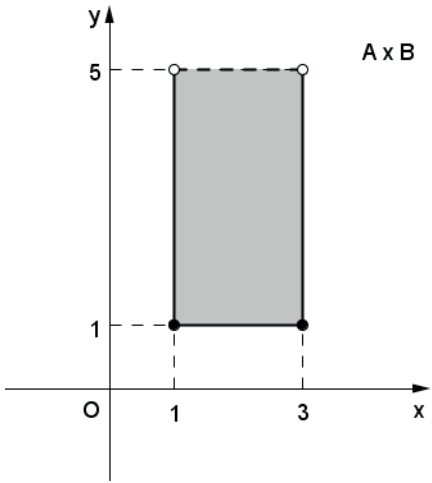
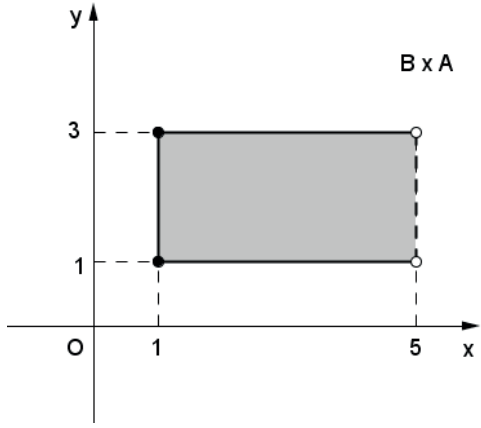
Exemplo 2: A=[1,3] e B=[1,5[
Propriedades do produto cartesiano:
A × (B ∪ C) = (A × B) ∪ (A × C)
A × (B ∩ C) = (A × B) ∩ (A × C)
A × (B – C) = (A × B) – (A × C)
RELAÇÃO
Uma relação R de A em B é qualquer subconjunto de A×B.
Quando R é uma relação de A em A, diz-se apenas que R é uma relação em A.
Numa relação de A em B, A é chamado conjunto de partida e B, conjunto de chegada. O conjunto de todas as primeiras coordenadas que pertencem a R é chamado domínio e o conjunto de todas as segundas coordenadas que pertencem a R é chamado imagem, ou seja, o domínio e a imagem são formados por elementos que efetivamente estão em algum par ordenado da relação.
D(R)⊂ A e Im(R) ⊂ B
Exemplo:
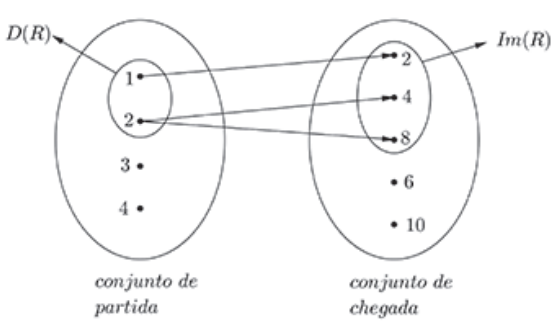
Sejam os conjuntos A = {1,2,3,4} e B={2,4,5,6,8,10}, então o conjunto R = {(1,2);(2,4);(2,8)} é uma relação de A em B, ou seja, R : A → B, cujo domínio é D(R) = {1,2} e a imagem Im (R)={2,4,8}.
FUNÇÃO
Observação: seja f uma relação de A em B, isto é, f ⊂ A × B, dizemos que f é uma função de A em B se, e somente se, para todo elemento A existe um e apenas um elemento y ∈ B tal que (x, y) ∈ f, ou seja, y = f(x).
Portanto, para que uma relação de A em B seja uma função, exige-se que a cada x ∈ A esteja associado um único y ∈ B. Entretanto pode existir y ∈ B que não esteja associado a nenhum elemento pertencente ao conjunto A ou que esteja associado a mais de um elemento de A.
Os dois diagramas seguintes representam relações de A em B, mas não funções de A em B. O primeiro porque existe um elemento de A que não está associado a nenhum elemento de B e o segundo porque existe um elemento de A que está associado a mais de um elemento de B.
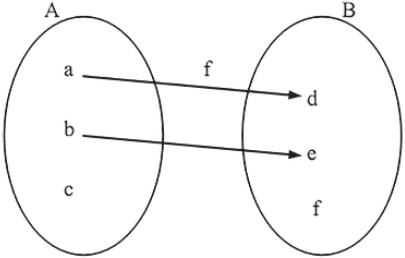
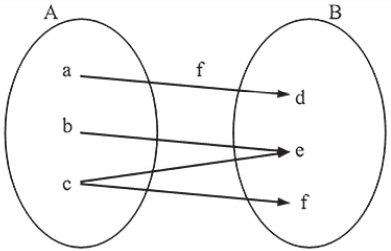
O diagrama de flechas a seguir representa uma relação de A em B que também é uma função de A em B.
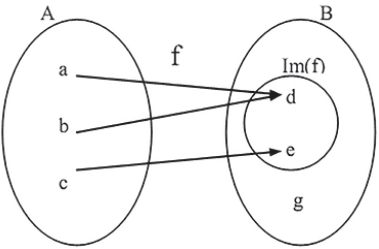

A análise do diagrama de flechas permite concluir que: f(a) = d, f(b) = d e f(c) = e.
O conjunto A é o domínio da função f e os seus elementos são os primeiros termos dos pares ordenados que constituem a função e a origem das flechas no diagrama.
O conjunto B é o contradomínio de f e os seus elementos são os segundos termos dos pares ordenados do produto cartesiano e os possíveis destinos das flechas.
O conjunto imagem é um subconjunto de B formado pelos elementos que são segundos termos dos pares ordenados da função ou o conjunto dos elementos que são efetivamente destino de flechas.
No diagrama anterior se deve observar que deve partir exatamente uma flecha de todo elemento do conjunto A. Já os elementos do conjunto B podem receber uma ou mais flechas ou até não receber nenhuma flecha.
Assim, o fato de d ∈ B ser imagem de dois elementos a e b de A não é empecilho para que f seja uma função de A em B.
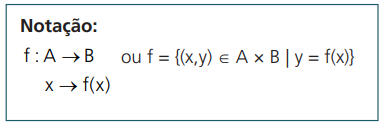
Chamam-se funções reais de variável real, aquelas cujo domínio e contradomínio são subconjuntos dos reais, ou seja, os pares ordenados (x, y) ∈ ℝ 2.
Nesse caso, costuma-se por comodidade definir a função apenas pela “regra de correspondência” e adota-se como domínio o maior subconjunto possível de ℝ.
Observação: em exercícios em que se pede o cálculo do domínio de uma função, em geral, o que se deseja é que seja apresentado o domínio máximo da função, ou seja, o maior conjunto para o qual aquela função está definida.
Exemplo: qual o domínio das funções a seguir?

Vamos identificar o domínio de validade dessas funções, ou seja, o maior subconjunto dos reais para os quais as funções estão definidas.

As funções reais de variável real podem ser representadas graficamente no plano cartesiano ortogonal. O gráfico da função é composto por todos os pares ordenados que compõem a função.
Observação: em virtude da definição de função, toda reta vertical, que passa por um ponto do domínio, intersecta o gráfico da função em exatamente um ponto.
Exemplo 1: a relação dada por x2 + y2 = 9 não é função, pois há retas verticais que intersectam o seu gráfico em dois pontos.
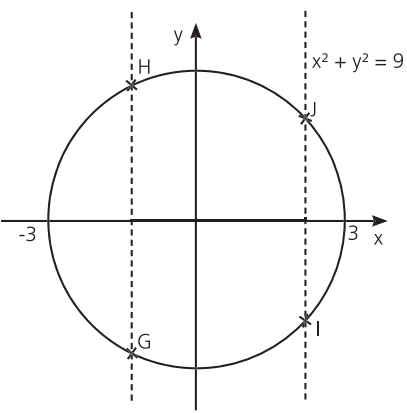
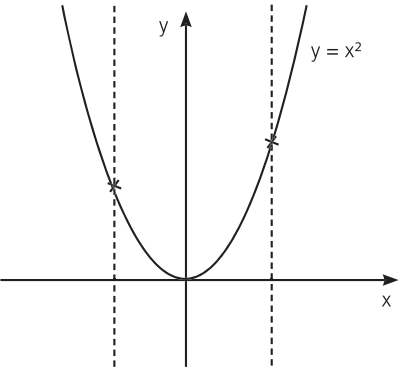
Exemplo 2: a relação y = x2 é uma função, pois as retas verticais traçadas a partir de pontos do domínio intersectam o gráfico em exatamente um ponto, ou seja, cada elemento do domínio possui exatamente uma imagem.
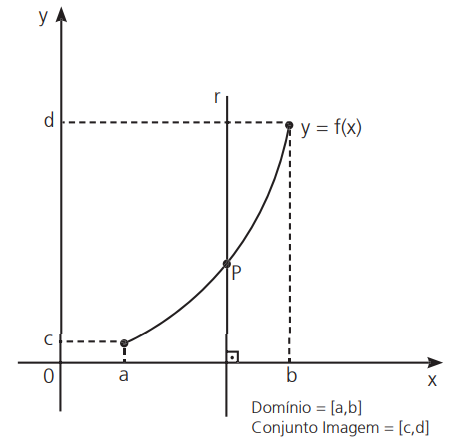
A análise do gráfico da função permite identificar o seu domínio e a sua imagem, como pode ser visto a seguir:
Zero ou raiz da função fé o número x ∈ D(f), cuja imagem é nula, isto é, f(x) = 0. Esses pontos são os pontos onde o gráfico da função f intersecta o eixo das abscissas (Ox).
É possível também identificar o sinal da função em cada trecho do domínio. Os pontos de imagem positiva encontram-se acima do eixo das abscissas (parte positiva do eixo das ordenadas) e os de imagem negativa abaixo (parte negativa do eixo das ordenadas).
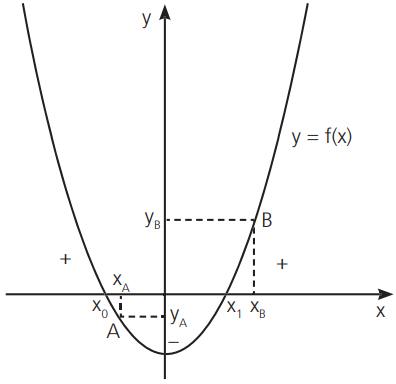
No gráfico acima, x0 e x1 são raízes. O ponto A tem ordenada yA < 0 e o ponto B ordenada yB > 0. Além disso, f(x) > 0 para x < x0 ou x > x1, e f(x) < 0 para x0 < x < x1.
Uma função f pode ser definida por várias sentenças abertas, cada uma das quais associada a um domínio Di ⊂ Df .
Exemplo:

Duas funções f e g são iguais se, e somente se, têm o mesmo domínio e f(x) = g(x) para todo x no domínio. Isso é equivalente a dizer que todos os pares ordenados que compõem as funções são iguais.

Por outro lado, f(x) = x+1 e

são iguais, pois possuem o mesmo domínio ℝ e o mesmo valor em todos os pontos.




