Dados os conjuntos A, B e C e as funções f : A → B, definida por y=f(x), e g : B → C, definida por z = g(y), chama-se função composta de g com f a função h = (g ∘ f); A → C, definida por:
Z=(g ∘ f)(x) = g(f(x))
Assim, a função (g ∘ f) pode ser entendida como uma função única que apresenta o mesmo resultado que as aplicações sucessivas de f e g.
O diagrama de flechas a seguir ilustra esse conceito:
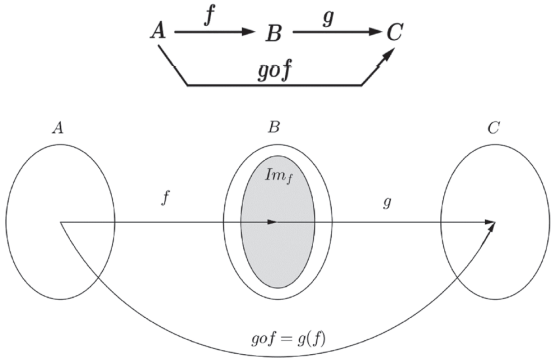
Na definição acima, adotamos o contradomínio de f coincidente com o domínio de g. No caso geral, a condição para que a função (g ∘ f) esteja definida é que a imagem de f esteja contida no domínio de g.
A composição de funções não é comutativa: g ∘ f ≠ f ∘ g. Pode acontecer, inclusive, de só uma das funções (f ∘ g) ou (g ∘ f) estar definida.
ProBizu: a sentença aberta que define (g ∘ f)(x) = g(f(x)) é obtida de g(x) substituindo-se x pela expressão de f(x).
Exemplo: sejam as funções reais f(x) = x2 + 4x – 5 e g(x) = 2 x – 3, calcule as expressões de (f ∘ g) e (g ∘ f).
(f ∘ g)(x) = f(g(x)) = f(2x – 3) = (2x – 3)2 + 4 · (2x – 3) – 5 = 4x2 – 4x – 8
(g ∘ f)(x) = g(f(x)) = g(x2 + 4x – 5) = 2 · (x2 + 4x – 5 – 3) = 2x2 + 8x – 13
TRANSLAÇÕES E TRANSFORMAC̣ÕES DE GRÁFICOS
TRANSLAC̣ÃO NA VERTICAL
Temos uma função f(x) tal que f : ℝ → ℝ e definimos a função g(x) = f(x) + a onde a ∈ ℝ. Dessa forma a função g(x) irá deslocar a função f(x), “a” unidades na vertical, sem alterar seu gráfico. Deslocará para cima quando a>0 e deslocará para baixo quando a < 0.
Exemplo: f(x) = x2 + 4x – 5
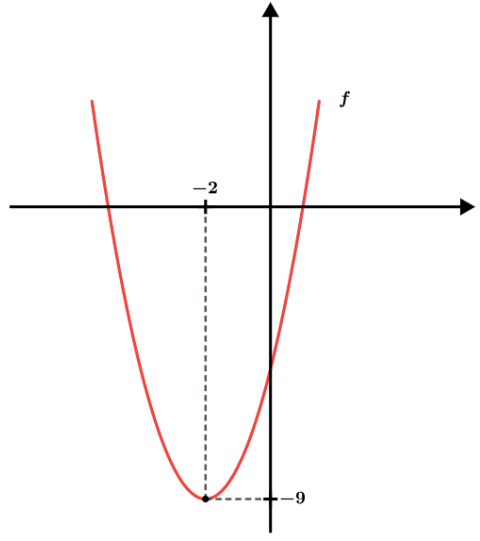
Ao fazermos a função g(x) = f(x) + 3 teremos a função g(x )= (x2 + 4x – 5) + 3 = x2 + 4x – 2
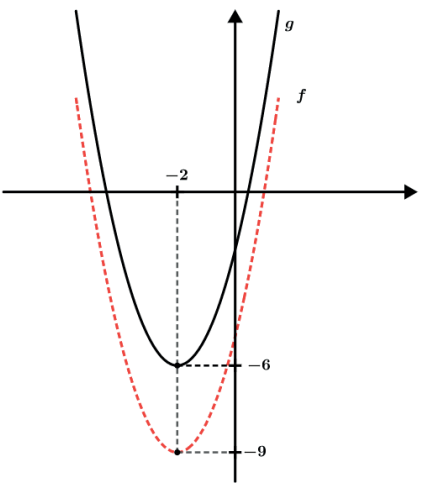
Percebemos que a função se movimentou 3 unidades para “cima”.
Então dessa forma podemos dizer que em g(x) = f(x) + a onde a ∈ ℝ temos que o gráfico “sobe” a unidades quando a > 0 e “desce” a unidades quando a < 0.
TRANSLAC̣ÃO NA HORIZONTAL
Temos uma função f(x) tal que f : ℝ → ℝ e definimos a função g(x) = f(x + b) onde b ∈ ℝ. Dessa forma a função g(x) irá deslocar a função f(x), “b” unidades na horizontal, sem alterar seu gráfico. Deslocará para esquerda quando b > 0 e deslocará para direita quando b < 0.
Exemplo: f(x) = x – 2
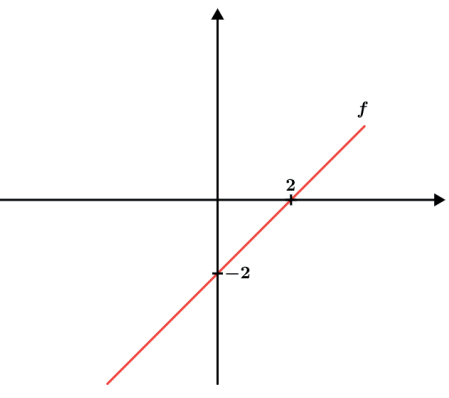
Agora quando definirmos a função g(x) = f(x + 2) devemos pensar o seguinte:
Para x = 0 teremos f(0) = 0 – 2 = -2 e g(0) = f(0 + 2) = f(2) = 2 – 2 = 0. Repare que a função f vem a ser 0 para x = 2, porém para a função g isso acontece em x = 0.
g(0) = f(2) = 0
Podemos pensar que ao fazer g(x) = f(x + 2) estaremos adiantando o que acontece com a função f em 2 unidades. Por exemplo a função g zera 2 unidades antes da função f, conforme a figura abaixo. Dessa forma:
g(2) = f(2 + 2) = f(4) = 4 – 2 = 2
O que para a função f acontece em x para a função g acontece em (x + 2).
Como se vê no gráfico que a função se desloca para esquerda.
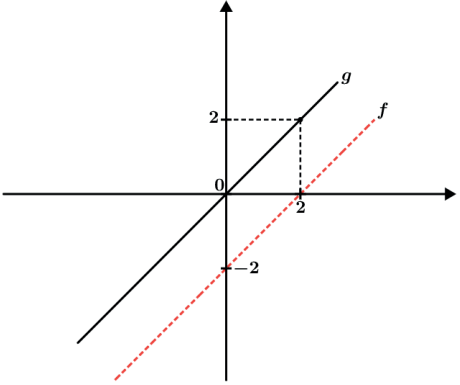
Então dessa forma podemos dizer que em g(x) = f(x + b) onde b ∈ ℝ temos que o gráfico “anda para a direita” b unidades quando b < 0 e “anda para a esquerda” b unidades quando b > 0.
Veja um outro exemplo para f(x) = x2 – 3x – 2 e g(x) = f(x – 3).
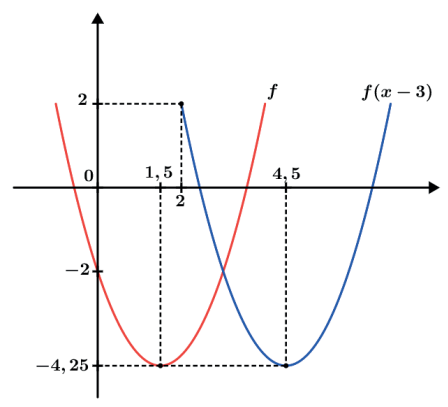
g(x) = |f(x)|
Ao se fazer g(x) = |f(x)| temos uma “modulação” da função f(x). Isso quer dizer que a função f(x) passa assumir somente valores positivos, sendo as partes negativas do gráfico sendo refletidas para cima do eixo Ox→.
Exemplo: f(x) = x2 – 3x – 2
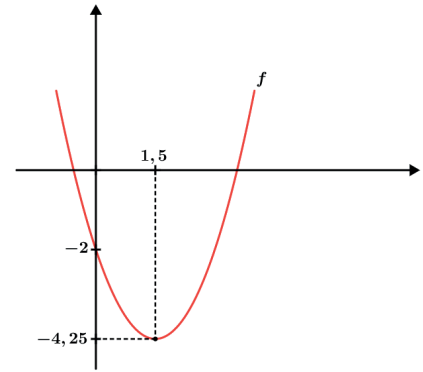
Fazendo g(x) = |f(x)| teremos:
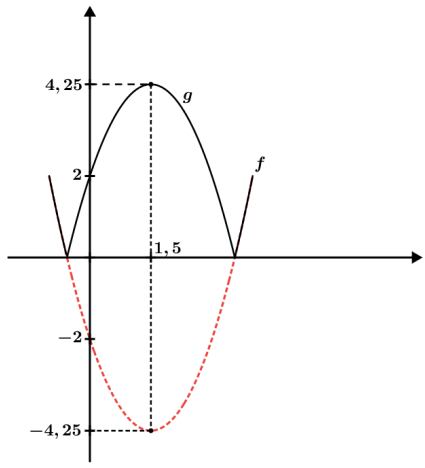
Vemos que a parte negativa da parábola foi completamente rebatida para cima do eixo Ox⇀ mantendo toda a simetria.
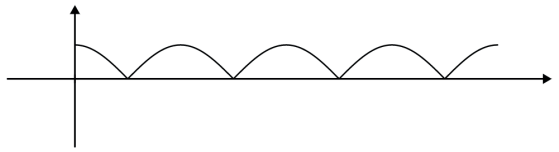
No gráfico abaixo vemos as funções cos x e |cos x| no intervalo de 0 a 4π.
f(x)= cosx
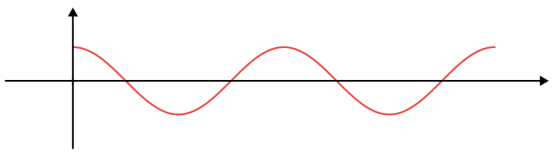
f(x) = | cosx |