DEFINIÇÃO
Um número complexo z é um número da forma z = x + yi.
A expressão x + yi é chamada forma algébrica de um número complexo z = (x, y) , podemos escrever o conjunto dos complexos da seguinte forma:
ℂ = {x + yi ∣ x ∈ ℝ, y ∈ ℝ ,i² = −1}
x = Re(z); parte real do complexo z.
y = Im(z); parte imaginária do complexo z.
Se x = 0 e y ≠ 0, z é um número imaginário puro.
Se y = 0, z é um número real.
OPERAÇÕES
Sejam z1 = x1 + y1i e z2 = x2 + y2i dois números complexos.
IGUALDADE
z1 = z2 ⇔ Re(z1) = Re(z2) e Im(z1) = Im(z2)
ADIÇÃO
z1 + z2 =(x1 + y1i) + (x2 + y2i) = (x1 + x2) + (y1 + y2)i
SUBTRAÇÃO
z1 − z2 = (x1 + y1i) − (x2 + y2i) = (x1 − x2) + (y1 − y2)i
MULTIPLICAÇÃO
z1 ⋅ z2 = (x1 + y1i) ⋅ (x2 + y2i) = (x1 ⋅ x2 − y1 ⋅ y2) + (x1 ⋅ y2 + x2 ⋅ y1)i
DEFINIÇÃO DO CONJUGADO DE UM NÚMERO COMPLEXO
Seja z um número complexo tal que z = x + yi. O número z = x + yi é chamado o conjugado do complexo z.
DIVISÃO
Sejam z = a + bi e w = c + di.

PROPRIEDADES

POTÊNCIAS DE I
Observe o cálculo das primeiras potências de i:
i0 = 1
i1 = i;
i2 = −1;
i3 = i2 · i = −i
i4 = i3 · i = 1
i5 = i4 · i = i
i6 = i5 · i = −1
i7 = i6 ⋅ i = −i
Percebe-se que as potências de i repetem-se de 4 em 4, iremos provar isto agora:
TEOREMA
in = i4q+r = (i4)q ⋅ ir = ir
Com n = 4 ⋅ q + r
Onde r é o resto da divisão de n por 4.
Portanto para calcular uma potência de i basta observar o resto da divisão de n por 4, e para isso basta utilizar o número formado pelos dois últimos algarismos de n.
PLANO DE ARGAND-GAUSS, MÓDULO, PROPRIEDADES, DISTÂNCIA
MÓDULO DE UM NÚMERO COMPLEXO
Seja z = x + yi então definimos seu módulo

PROPRIEDADES

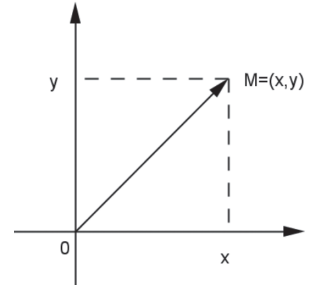
Um número complexo z cuja forma algébrica é x + yi pode ser representado no plano cartesiano R × R pelo ponto M = (x, y). O ponto M é então chamado de afixo do complexo z. Desta forma, podemos enxergar o complexo z como sendo o vetor OM→ e assim fica perfeitamente plausível a definição que demos para o módulo do complexo z pois

LUGARES GEOMÉTRICOS
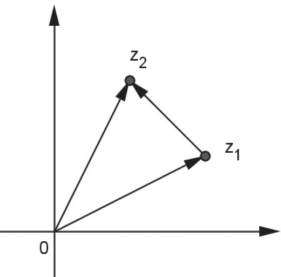
Sejam z, z1, z2 ∈ ℂ, então o módulo |z2 − z1| representa a distância do afixo z1 ao afixo z2.
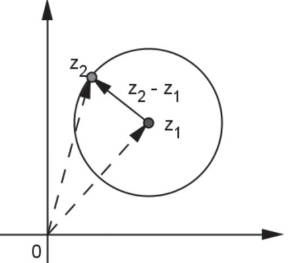
a) O conjunto dos pontos tais que |z − z1| = ré uma circunferência de centro em z1 e raio z2.
b) O conjunto dos pontos tais que |z − z1| = |z − z2| é a mediatriz do segmento z1z2.
c) O conjunto dos pontos tais que |z − z1| + |z − z2| = 2a, com 2a > |z1 − z2| é uma elipse com focos em z1 e z2 e eixo maior igual a 2a.
d) O conjunto dos pontos tais que |z − z1| – |z − z2| = 2a, com 2a < |z1 − z2| é um ramo de hipérbole com focos em z1, z2.




