Como há aceleração, podemos dizer que a soma das forças que atuam no corpo é diferente de zero. Ou seja, quando um corpo está realizando uma trajetória curvilínea, sofrerá a atuação de forças. A resultante das forças será diferente de zero.
Já estudamos que, para o módulo da velocidade não mudar, o vetor aceleração deve apontar para o centro, recebendo o nome de aceleração centrípeta. Então, como o vetor aceleração aponta para o centro, a resultante das forças também apontará para o centro.
Como
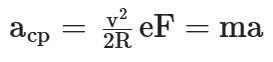
A resultante das forças (como aponta sempre para o centro, é chamada de Resultante Centrípeta, Rcp) vale:
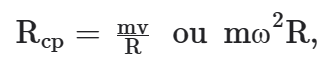
já que
v = ωR
Vamos ver algumas trajetórias e as forças atuantes:
CURVA PLANA
Neste caso, podemos imaginar um carro fazendo uma curva. Podemos imaginar até mesmo, de maneira simplificada, o movimento de translação dos planetas ao redor do Sol, ou o da Lua ao redor da Terra.
É o atrito entre o pneu e o asfalto que irá possibilitar que o carro realize uma curva sem deslizar (derrapar). Repare que, nesse caso, atuam três forças no carro: peso, normal e atrito. As duas primeiras atuam na vertical e em sentidos opostos, possuindo o mesmo módulo. A força de atrito é que está perpendicular ao vetor velocidade, apontando para o centro da trajetória. Então:
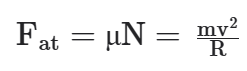
Como, nesse caso, P = N
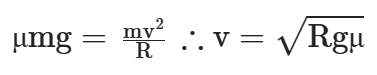
Perceba que, quanto menor o coeficiente de atrito entre o pneu e o asfalto, menor deve ser a velocidade do carro, para que realize a curva sem deslizar. Lembrando que, sem deslizar, significa que estamos usando o coeficiente de atrito estático. (A roda do carro não desliza no asfalto. Veja que a distância entre o carro e o centro da curva é sempre a mesma, que é o próprio raio R da curva).
No caso entre a Lua e a Terra, a única força que atua na Lua para que ela realize a trajetória é a força gravitacional, que aponta para o centro da trajetória. Logo:
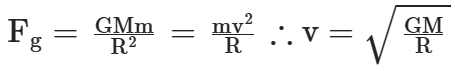
Essa é a velocidade orbital da Lua. Se estudássemos o sistema Terra-Sol, essa seria a velocidade orbital da Terra, na qual M seria a massa do Sol e R, o raio da órbita (distância média Terra-Sol).
Mais tarde, iremos estudar gravitação universal. Está aqui apenas como curiosidade.
CURVA INCLINADA SEM ATRITO

(Disponível em: http://fisicacuriosaecriativa.blogspot.com/2012/09/por-que-temos-de-fazer-forca-para.html)
Nessa situação, as forças que atuam no ônibus são Peso e Normal, igual à situação de plano inclinado, ou seja, Peso atuando na vertical e a Normal, normal ao plano. A resultante das forças aponta para o centro da trajetória. Nesse caso, está apontando na horizontal para a esquerda. Veja:
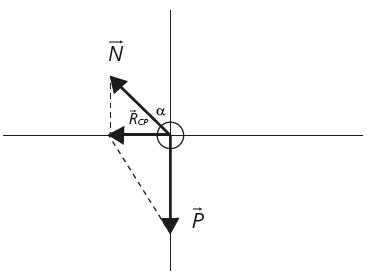

Então:
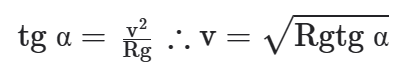
Observe que, se a curva possuir atrito, duas situações são possíveis: o carro pode estar em alta velocidade, na iminência de escorregar para fora da pista. Nesse caso, o atrito aponta para dentro da pista, paralelo ao plano inclinado ou a velocidade é baixa, fazendo com que esteja na iminência de escorregar para baixo. Nesse caso, o atrito aponta para fora da pista, paralelo ao plano inclinado. A relação acima não seria mais válida.
PÊNDULO SIMPLES
Esse movimento será estudado com mais detalhes no módulo sobre movimento harmônico simples (M.H.S.). O que temos que ver, por enquanto, é que a velocidade do pêndulo muda a cada instante. No momento em que é abandonado, a sua velocidade é zero e, na parte mais inferior, a sua velocidade será máxima. Ou seja, além de haver uma aceleração apontando o tempo todo para o centro da trajetória, há também uma aceleração na tangente da trajetória. Na parte da queda, essa aceleração aponta no mesmo sentido de vetor velocidade. Por sua vez, quando o pêndulo passa pela posição de maior velocidade, iniciando a sua subida, a aceleração tangencial passa a apontar para o sentido oposto ao da velocidade.
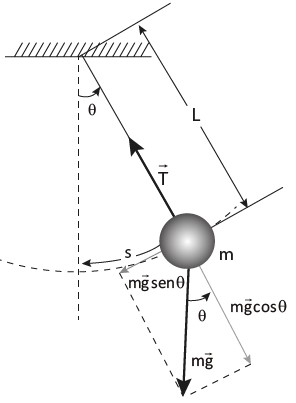
O pêndulo simples e as forças atuantes consideradas na modelagem simplificada.
Na situação acima, as forças que atuam na direção radial são a tração e uma componente da força peso. A tração aponta para o centro e a componente do peso, para fora. Como a resultante aponta para o centro, temos que:
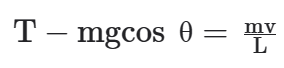
Perceba que, a cada instante, θ e v mudam. A equação para o ponto inferior seria:
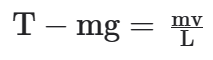
Já para os extremos, onde a velocidade é nula, seria:
T = mgcosθ
Basta imaginarmos que a figura acima retrata esse momento, no qual a velocidade é nula.
PÊNDULO CÔNICO
Nesse caso, o nosso pêndulo realiza uma curva plana, sofrendo a atuação de duas forças apenas: tração e peso.
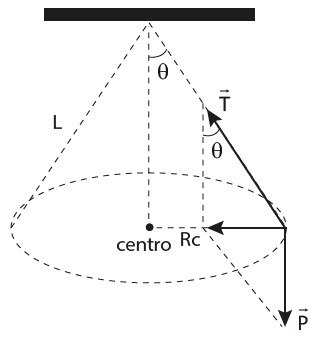
Note que, durante toda a trajetória, a resultante aponta para o centro. Com o auxílio da figura acima, podemos ver que a resultante centrípeta é a componente seno da tração:
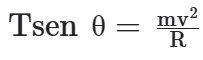
E, como não há movimento na vertical:
T cosθ = P
Então:
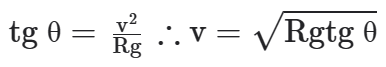
Note que esse movimento é semelhante ao da curva inclinada, trocando apenas a normal pela tração.
GLOBO DA MORTE
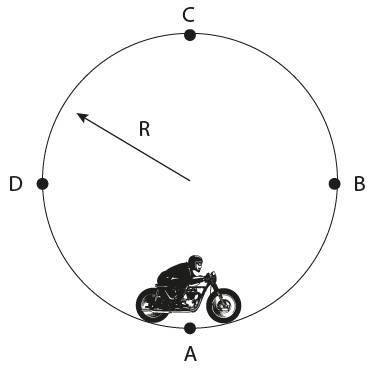
O movimento é semelhante ao de um avião fazendo um looping. O que se deseja saber nesse tipo de movimento é a velocidade mínima que o ciclista/piloto (avião) deve ter para conseguir realizar uma volta completa. Podemos notar que essa velocidade é maior em A do que em C. O que acontece no ponto C?
Nesse ponto, o móvel sofre duas forças: peso e normal. As duas apontam para baixo. Por isso, é muito difícil conseguir dar a volta sem cair. Como estamos preocupados com a velocidade mínima, podemos dizer que, qualquer valor abaixo desta, ela irá cair, ou seja, está na iminência de perder o contato com a pista, de perder a normal. Então, no ponto C, podemos dizer que a moto está perdendo o contato com a pista (se fosse um avião realizando um looping, poderíamos dizer que o piloto está perdendo o contato com o seu assento). Sendo assim, a única força atuante nesse ponto será o Peso, que aponta para o centro da trajetória:
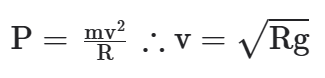
Qual seria, então, a velocidade mínima que ele deve ter no ponto A?
Podemos descobrir usando Torricelli:
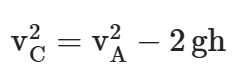
Em que:
h = 2R
Logo:
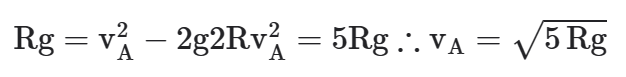
QUEBRA-MOLAS E DEPRESSÕES
Nos quebra-molas, o carro sofre a atuação de duas forças: peso e normal. Podemos considerar que a trajetória de um carro ao passar por um quebra-molas é, aproximadamente, um semicírculo. Note que o vetor peso aponta para o centro dessa trajetória e o vetor normal aponta para fora. Como se trata de uma trajetória curvilínea, o vetor força resultante aponta para o centro da trajetória, ou seja, o módulo do peso supera o da normal.
Vamos supor que antes de o carro passar por um quebra-molas estava em uma trajetória retilínea. Então, o módulo do peso era igual ao da normal. Ao passar pelo quebra-molas, o peso do carro não muda, mas o módulo da normal vai diminuindo. Significa que a força de contato entre as pessoas que estão dentro do carro e os seus assentos diminui. Sabemos que, quando um carro está em alta velocidade e passa por um quebra-molas, as pessoas dentro do carro perdem o contato com os seus assentos, chegando a bater no teto! Então, deve haver uma relação matemática entre a velocidade do carro e a normal:
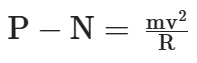
Note que, quanto maior o valor da velocidade, menor será o módulo do vetor força de contato (normal). Para que as pessoas percam completamente o contato com os seus assentos:
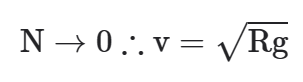
Mas, quando um carro passa por uma depressão, o módulo da normal é maior que o do peso:
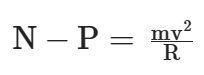
Como o peso é constante, quanto maior a velocidade do carro, maior será a força de contato (as pessoas dentro do carro ficam mais “grudadas” nos seus assentos). A sensação é semelhante a de estarmos dentro de um elevador subindo aceleradamente (N – P = m · a). Já no quebra-molas, poderíamos associar com o que sentimos quando estamos dentro de um elevador que desce aceleradamente (P – N = m · a). Se o cabo do elevador se rompesse, perderíamos o contato com o piso (estaríamos em queda-livre).





