Figuras equivalentes são aquelas que possuem a mesma área.
Se dois triângulos possuem bases e alturas congruentes, então eles são equivalentes.
Se dois triângulos são semelhantes, então a razão entre suas áreas é o quadrado da razão de semelhança.
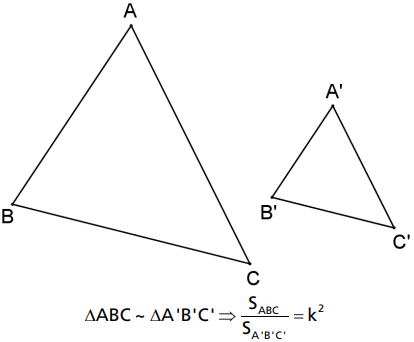
onde k é a razão de semelhança.
Demonstração:
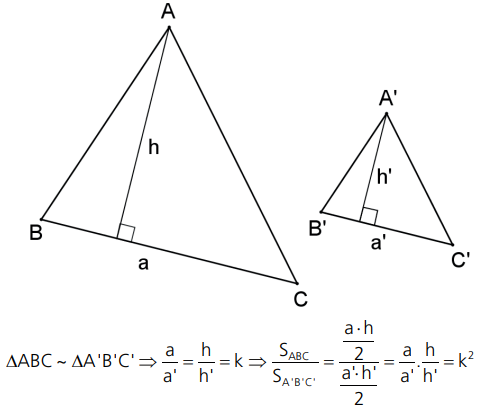
Note que essa propriedade vale para quaisquer figuras semelhantes, não só para triângulos.
Exemplo:
Sejam M e N pontos médios dos lados AB e AC, respectivamente, de um triângulo ABC. Calcule a razão entre as áreas dos triângulos AMN e ABC.
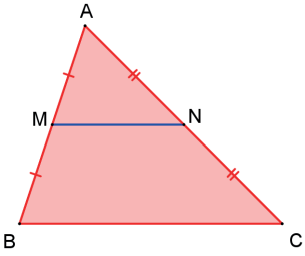
MN é base média do triângulo ABC, então MN || BC e MN = BC/2.

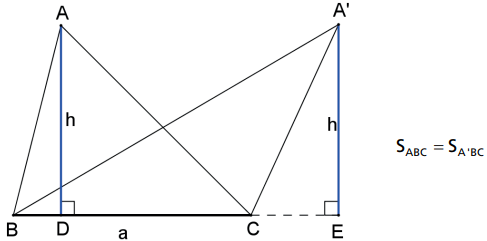
Se dois triângulos possuem bases sobre a mesma reta e vértice comum, então a razão entre suas áreas é igual à razão entre suas bases.
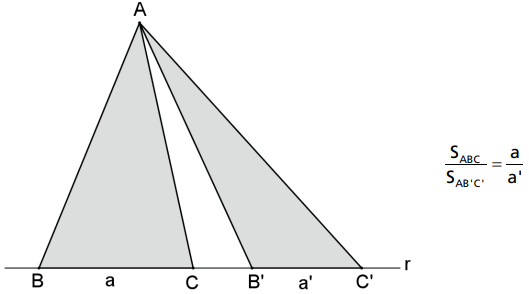
Demonstração:
Seja h a distância do ponto A à reta r então h é altura do ΔABC e do ΔAB’C’.

Uma consequência imediata da proposição anterior é que a razão entre as áreas em que uma ceviana divide um triângulo é igual à razão entre as medidas dos segmentos em que essa ceviana divide o lado, ou seja:

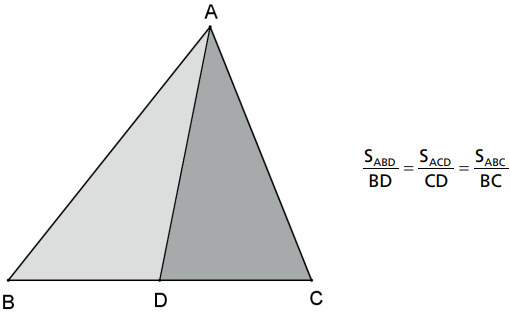
Exemplo:
Seja um triângulo ABC de lados AB=4 e AC=5, e o ponto D sobre BC é o pé da bissetriz do ângulo A^. Calcule a razão entre as áreas dos triângulos ABD e ACD.
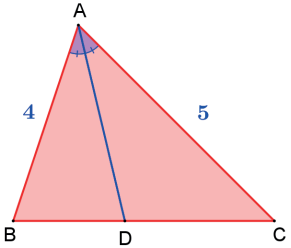
Pelo teorema da bissetriz interna, temos:

A razão entre as áreas dos triângulos ABD e ACD é:

Se dois triângulos possuem base comum e o vértice de um deles pertence a uma ceviana do outro partindo do vértice oposto à base comum, então a razão entre a área do maior e do menor deles é igual à razão entre a medida da ceviana e a medida da parte entre o vértice do menor e a base comum.
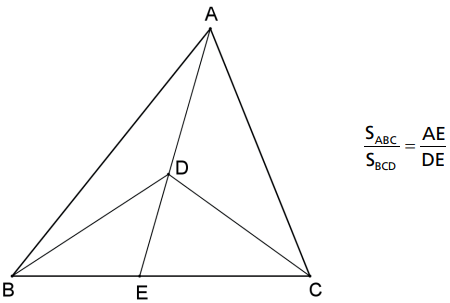
Demonstração:

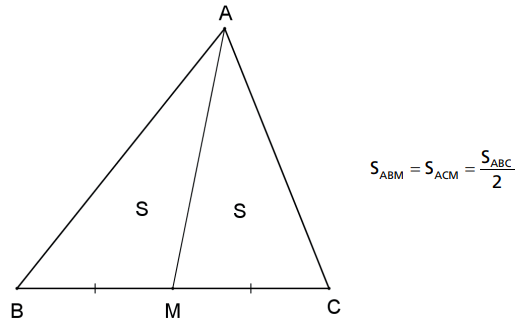
Uma mediana divide o triângulo em duas regiões equivalentes.
Seja AM a mediana relativa ao lado BC do ΔABC.
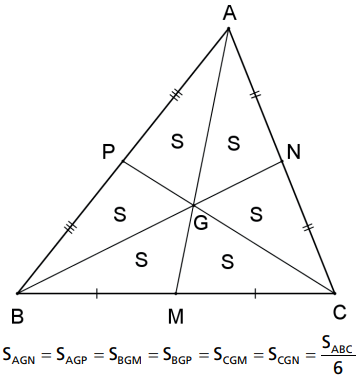
As três medianas de um triângulo dividem esse triângulo em seis triângulos equivalentes.
Sejam AM, BN e CP as medianas do ΔABC, então
Demonstração:
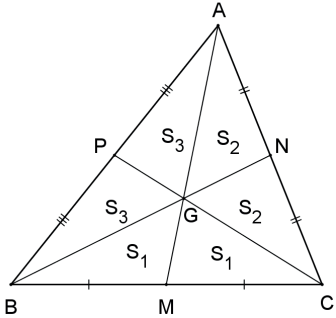
Como M, N e P são pontos médios, então os ΔBGC, ΔAGC e ΔAGB são divididos em duas áreas equivalentes S1, S2 e S3, respectivamente.

As três bases médias de um triângulo dividem o triângulo em quatro regiões equivalentes.
Sejam M, N e P os pontos médios dos lados do ΔABC, então
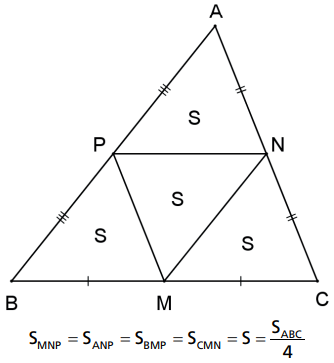
Demonstração:
Basta observar que ΔMNP ≡ ΔANP ≡ ΔBMP ≡ ΔCMN.
As três medianas e as três bases médias de um triângulo dividem o triângulo em 12 triângulos, 6 deles equivalentes a 18 da área do triângulo e 6 deles equivalentes a 1/24 da área do triângulo.
Sejam M, N e P os pontos médios dos lados do ΔABC, então
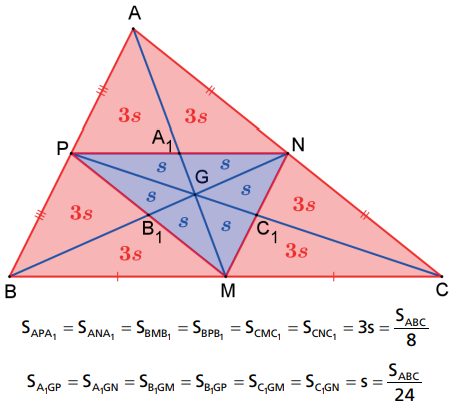
Demonstração:
Os pontos A1, B1 e C1 são pontos médios de PN, MN e MP, respectivamente.

Analogamente, temos

Analogamente, prova-se para os outros triângulos.
A bissetriz de um dos ângulos de um triângulo divide-o em dois triângulos cujas áreas estão na mesma razão que os lados adjacentes ao ângulo.
Seja AD a bissetriz do ângulo  do ΔABC, então
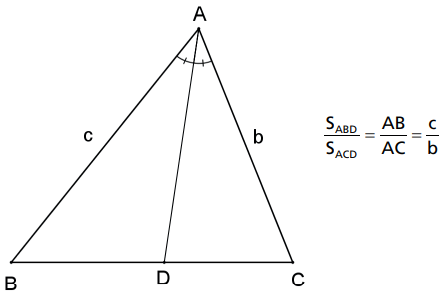
Demonstração:
Pelo teorema das bissetrizes, temos:

Se dois triângulos possuem um ângulo comum, então a razão entre suas áreas é igual à razão entre os produtos dos lados adjacentes a esse ângulo.
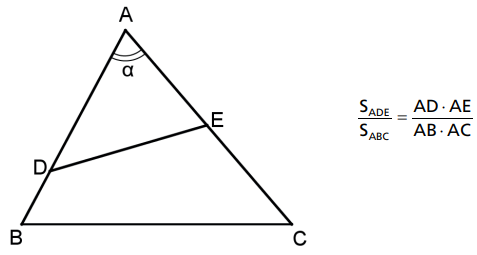
Demonstração:





