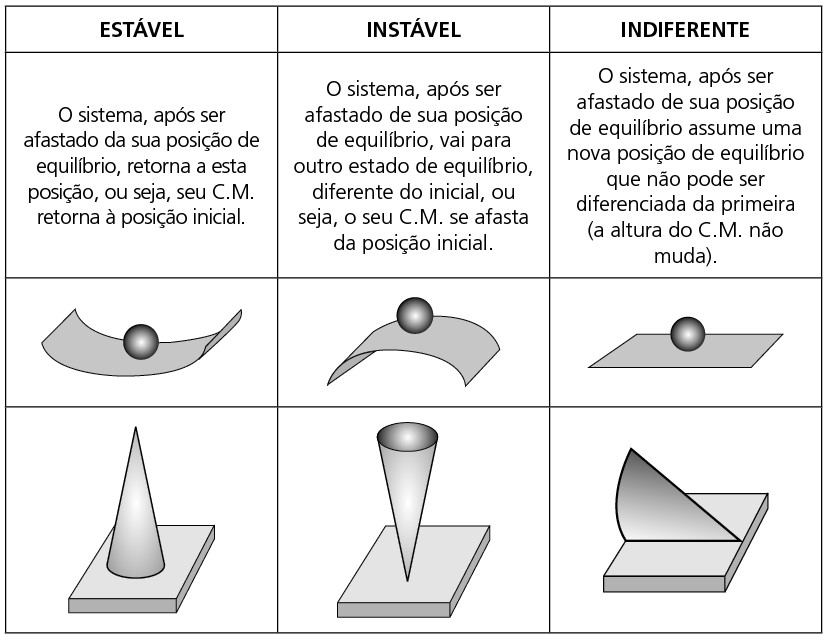
TIPOS DE EQUILÍBRIO
Observação: TEOREMA DAS TRÊS FORÇAS
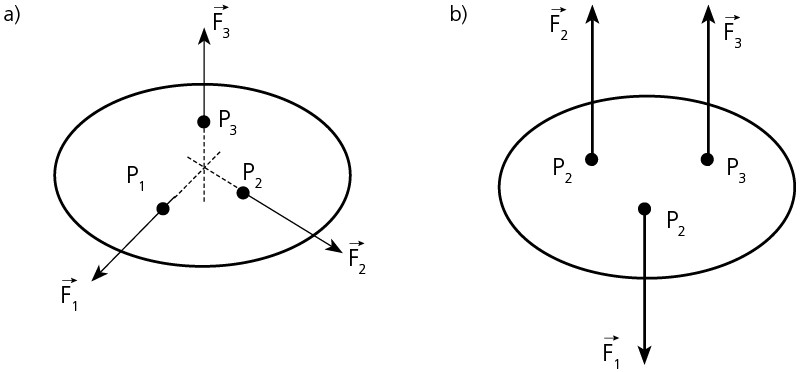
Um corpo está em equilíbrio sob ação exclusiva de três forças. Estas deverão ser coplanares e suas linhas de forças de ação serão, necessariamente, concorrentes (a) em um único ponto ou paralelas (b).
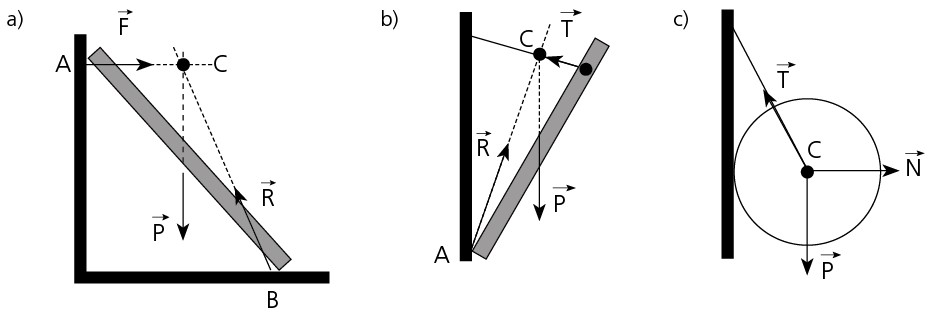
Exemplo:
APROFUNDAMENTO
MOMENTO ANGULAR (L)
Não confundir momento da força ou torque com momento angular (L). Esta é outra grandeza física vetorial. O torque mede a variação de momento angular (∆L) por unidade de tempo (∆t). Quando um corpo extenso sofre um torque resultante, sofrerá uma aceleração angular, em relação ao seu eixo de rotação:

Então:

Grandeza vetorial conhecida como momento linear ou quantidade de movimento (p). A estudaremos com mais detalhes mais para frente.
Sendo assim:

Quando o corpo está em equilíbrio, ou seja, quando o torque resultante for zero, não haverá variação do momentum angular, ou seja, o momento angular permanece constante. O momento angular está para o momento linear assim como o torque está para a força.
Observação: No movimento sob a ação de forças centrais, o momento angular se conserva, de modo que a velocidade areolar é constante: o raio vetor que liga a partícula ao centro de forças descreve áreas iguais em tempos iguais. Essa conclusão é conhecida como 2ª Lei de Kepler, que nada mais é do que a lei de conservação do momento angular. Um exemplo é o movimento de translação da Terra ao redor do Sol:
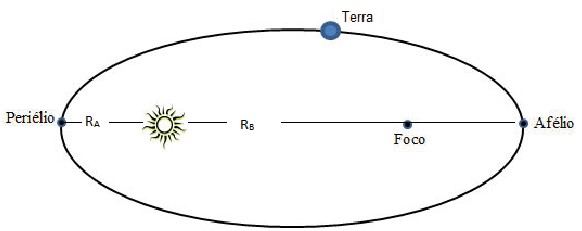
Quando o planeta está no afélio (ponto mais afastado) e no periélio (ponto mais próximo), o vetor velocidade é perpendicular ao raio vetor. Conservando o momento angular:

A velocidade será máxima no periélio e mínima no afélio.
MOMENTO DE INÉRCIA (I)
Sabemos que, se uma força F for aplicada em um corpo extenso de massa m, a uma distância r do seu eixo de rotação, a componente perpendicular dessa força pode fazê-lo girar com uma aceleração angular α. Essa aceleração vai depender de qual corpo estamos rotacionando. Do seu formato, de onde está sendo aplicada a força e da sua massa. A “dificuldade” de fazer um objeto rotacionar (ou de mudar a sua rotação, parando-a, por exemplo) chama-se momento de inércia (I):

Vamos imaginar um cilindro circular de massa m e raio r em um plano inclinado cujo ângulo de inclinação em relação ao piso horizontal vale θ. A força de atrito entre o piso e o cilindro pode fazer com que ele comece a rolar ao longo do piso (se não houver atrito ele só desliza) sem deslizar. O torque do atrito é responsável pela aceleração angular do cilindro. Se fosse uma esfera maciça de raio r, a aceleração angular que ela teria seria diferente, por exemplo:

Observação: Se a resultante dos torques for nula, não teremos aceleração angular, ou seja, a velocidade angular do sistema será constante:

Essa é a física de uma patinadora de gelo, por exemplo. Ela encolhe os seus braços para girar mais rapidamente:

Diminuindo o momento de inércia (I), ao encolher os braços, a sua velocidade angular ω aumenta. O mesmo acontece com uma bailarina, para fazer várias piruetas, ou um mergulhador, que dá um salto múltiplo dobrando os joelhos e juntando os braços para girar o corpo e o gato, que gira a cauda e encolhe as patas, para cair de pé.




