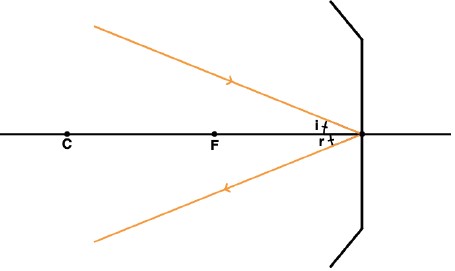
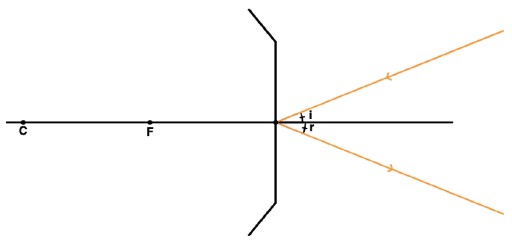
Um espelho esférico pode conjugar infinitas imagens de um ponto P.
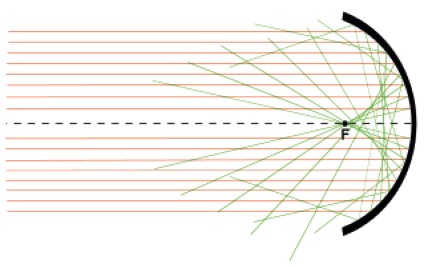
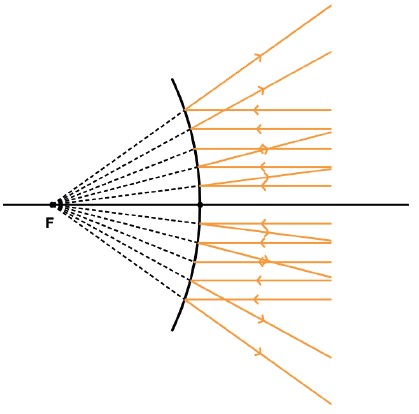
Dessa forma para cada um dos raios luminosos distintos que partem de P e que se refletem no espelho, haverá a formação de diversos pontos imagens distintos. Isso formará uma mancha luminosa denominada cáustica de reflexão.
Para evitar isso, usaremos os espelhos gaussianos, cuja abertura é muito pequena, menor que 10°.
FOCO DE UM ESPELHO GAUSSIANO
O foco principal (F) é o ponto de convergência de raios incidentes paralelos entre si e ao eixo principal e fica na metade do caminho entre o centro e o vértice.
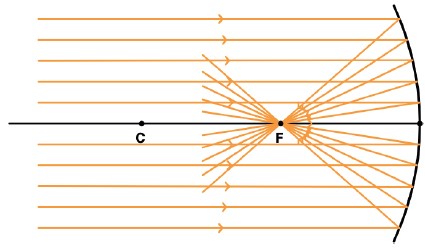
O foco de um espelho esférico fica entre o centro de curvatura (C) e o vértice (V) sendo o foco F o ponto médio do segmento CV.
Sendo a distância do vértice V ao centro de curvatura C chamada de raio de curvatura R.
CV = R
Teremos que
CF = VF = R/2
FOCO SECUNDÁRIO
Suponha agora que um feixe de raios luminosos paralelos entre si e oblíquos ao eixo principal. Dessa vez, os raios refletidos também convergem em um mesmo ponto, denominado foco secundário. Esse foco fica num plano perpendicular ao eixo principal que passa pelo foco principal.
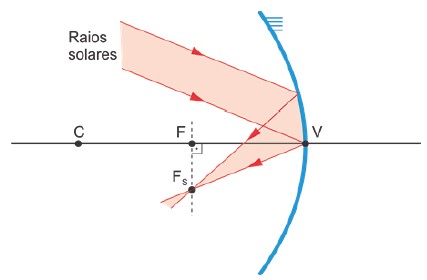
Foco secundário de um espelho côncavo
RESUMO DAS PROPRIEDADES DOS ESPELHOS ESFÉRICOS DE GAUSS
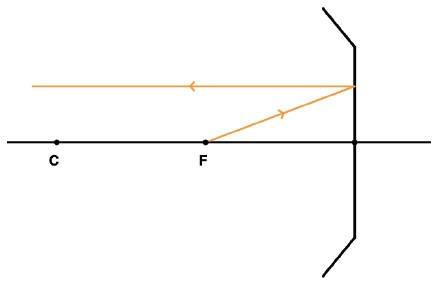
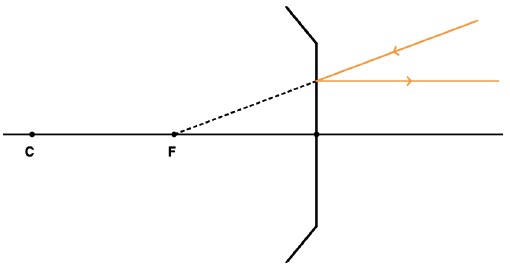
Todo raio que incide paralelamente ao eixo principal é refletido passando pelo foco (F).
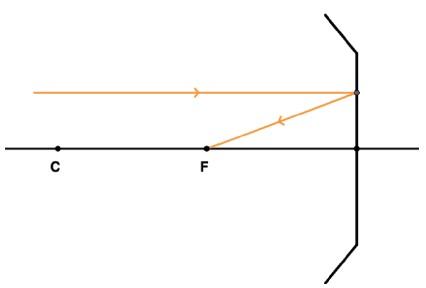
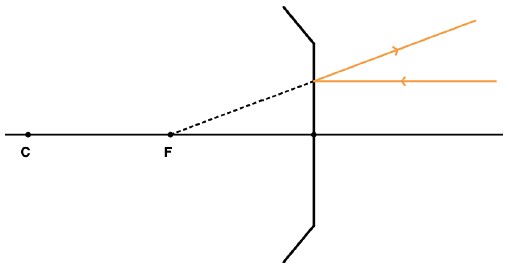
Todo raio que incide passando pelo foco é refletido paralelamente ao eixo principal.
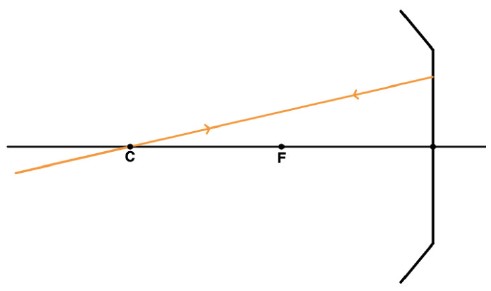
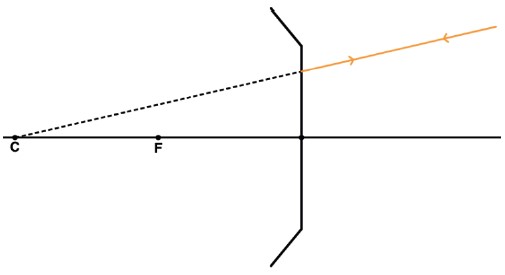
Todo raio que incide sobre o centro de curvatura (C) é refletido sobre si mesmo.
Todo raio que incide sobre o vértice é refletido simetricamente a ele, ou seja, i = r.