DEFINIÇÃO
Chama-se esfera a um sólido limitado por uma superfície em que todos os pontos de um ponto interior chamado de centro.
A superfície que delimita a esfera, denomina-se: superfície esférica e qualquer segmento OP que une o centro O com um ponto P da superfície esférica denomina-se raio da esfera.
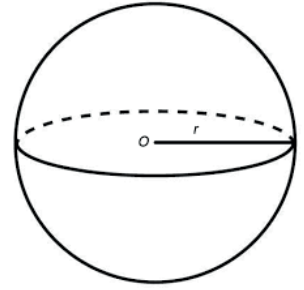
ÁREA DA SUPERFÍCIE ESFÉRICA DE RAIO R
A área da superfície esférica é igual ao quádruplo da área do círculo máximo da esfera que tem área igual a πR2. Portanto a área da superfície esférica é S = 4πR2.
VOLUME DA ESFERA
O Volume da esfera de raio R é igual ao produto de 4/3 do raio pela área do círculo de área máxima logo seu volume é dado pela fórmula V = 4/3 πR3.
FUSO E CUNHA ESFÉRICA
Denomina-se fuso esférico a superfície gerada pela rotação de uma circunferência que gira um ângulo αα menor que 2π radianos ao redor do seu diâmetro.
Chama-se cunha esférica ao sólido gerado pela rotação, de um ângulo α, menor que 2π radianos, de um semicírculo, ao redor do seu diâmetro.
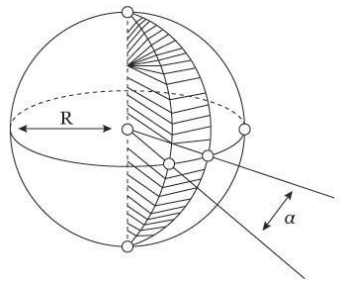
A área do fuso esférico e o volume da cunha esférica são proporcionais ao ângulo do fuso αα.
Área do fuso esférico de ângulo α radianos: Sfuso = 2 · α · R2.
Volume da cunha esférica de ângulo α radianos: Vcunha = 2/3 · α · R3.
SEGMENTO E CALOTA ESFÉRICA
Quando seccionamos uma esfera por um plano e um outro plano tangencia a esfera, o plano secante divide a esfera em dois segmentos esféricos, e a superfície esférica em duas calotas esféricas.
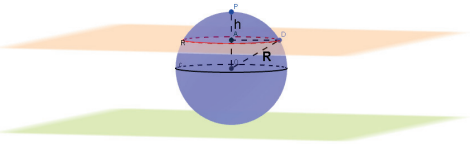
VOLUME DO SEGMENTO ESFÉRICO
De modo análogo ao volume da esfera, podemos calcular o volume do segmento esférico de altura h subtraindo um tronco de cone de altura h, de um cilindro de raio R e também altura h.
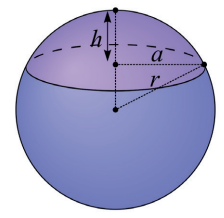
Volume do segmento esférico de altura h em uma esfera de raio r.

Também podemos calcular como

Área da calota esférica de altura h em uma esfera de raio R

Observação:
O VOLUME DA ESFERA PELO PRINCÍPIO DE CAVALIERI
Vamos inicialmente definir a anticlepsidra.
A anticlepsidra é sólido geométrico formado a partir de um cilindro equilátero, do qual subtraímos dois cones opostos pelos vértices (como uma ampulheta) cujas bases coincidam com as bases do cilindro e cuja altura, obviamente, seja igual ao raio da base.

Agora tomemos uma esfera e uma anticlepsidra, de mesmo raio r, assentadas num mesmo plano horizontal.
Pelo princípio de Cavalieri se as seções dos sólidos, obtidas a uma mesma altura, têm a mesma área, então os sólidos têm o mesmo volume.
De acordo com a figura acima tomamos uma seção transversal por um plano αα a partir de uma altura h tomado a partir dos centros da esfera e da anticlepsidra.
Vamos calcular as áreas das 2 seções que estão assinaladas em verde na figura.
I. Área da seção determinada na esfera.
Do Teorema de Pitágoras no triângulo retângulo de lados r, s e h temos
r2 = h2 + s2 ⇒ s2 = r2 − h2
Logo a área do círculo delimitado pelo plano αα é
S = πs2 = πr2 − h2
II. Área da seção determinada na anticlepsidra.
A área determinada pelo plano αα na anticlepsidra é a área da coroa circular assinalada em verde.
S = πr2 − πh2 = πr2 − h2
Logo vemos que as áreas delimitadas por qualquer plano paralelo ao plano horizontal onde estão situadas a esfera e a anticlepsidra são iguais e assim a esfera terá o mesmo volume da anticlepsidra.
Assim o volume da esfera será

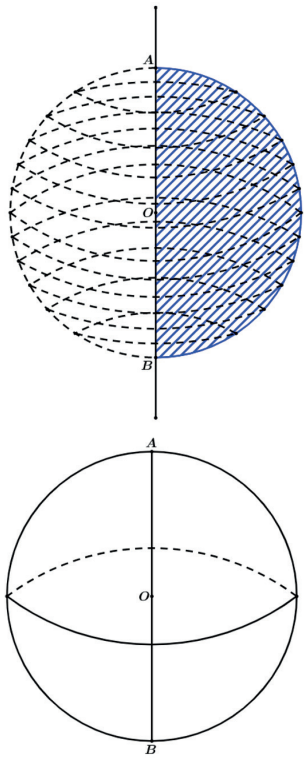
ESFERA DE REVOLUÇÃO
A esfera é obtida pela rotação de um semicírculo ou um círculo completo em torno de seu diâmetro.
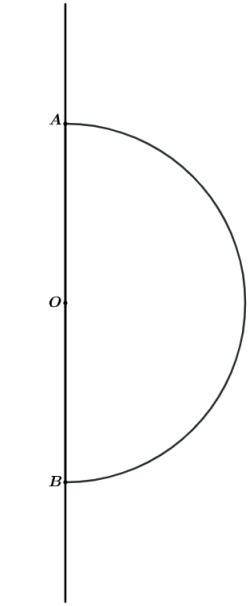
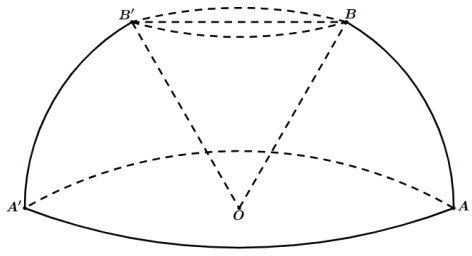
Vamos ilustrar um sólido de revolução “diferente” já cobrado em concurso militar. Vamos ver o resultado da rotação de 360° de um setor circular.
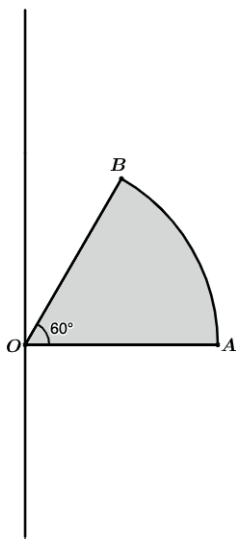
Vamos rotacionar o setor circular OAB em torno do eixo especificado.
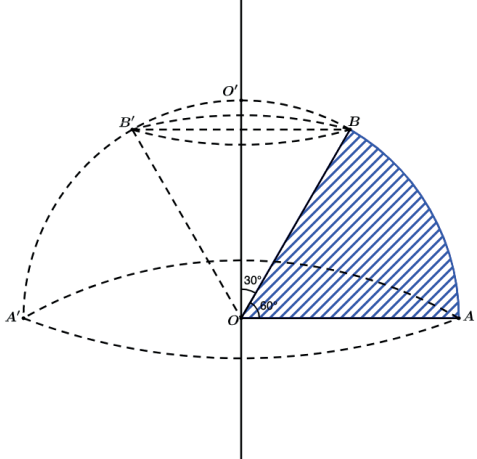
Teremos como volume final o volume da semiesfera AO’A’ de centro O subtraído do volume do cone reto OBB’ e também subtraído do volume da calota esférica BO’B’.