Equações Trigonométricas básicas

EQUAÇÃO EM SENO

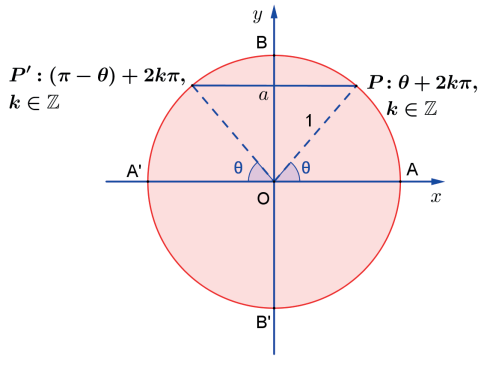
Seja a ∈ ℝ tal que |a| ≤ 1, então sen α = a ⇔ α = arcsen a + 2kπ, k ∈ ℤ ∨ α = π – arcsen a + 2kπ, k ∈ ℤ.

Notação resumida: α = kπ + (-1)^k · arcsen a, k ∈ ℤ

Observe que representamos a solução da equação utilizando a função arco seno por se tratar de um caso geral. Na maioria dos problemas são apresentados ângulos cujos valores das linhas trigonométricas são conhecidos.

Ao resolver uma equação trigonométrica, é sempre útil identificar as soluções no ciclo trigonométrico, como na figura seguinte.

Exemplo 1:

sen2x = ¹/₂ ⇔ 2x = kπ +(-1)^k · ^π/₆, k ∈ ℤ ⇔ x = ^kπ/₂ + (-1)_k · ^π/₁₂, k ∈ ℤ

Se, na equação sen α = a, o valor de a for tal que |a| > 1, então o conjunto solução da equação é vazio.

Exemplo 2:

sen x = 2 ⇔ S = ∅

Exemplo 3:

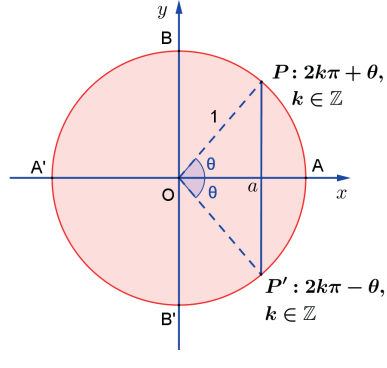
EQUAÇÃO EM COSSENO

Seja α ∈ ℝ tal que |a| ≤ , então

cosα = a ⇔ α = 2kπ ± arccosa, k ∈ ℤ

A identificação das soluções da equação no ciclo trigonométrico encontra-se na figura seguinte.

Exemplo 1:

cos2x = ¹/₂ ⇔ 2x = 2kπ ± ^π/₃ , k ∈ ℤ ⇔ x= kπ ± ^π/₆ , k ∈ ℤ

Se, na equação αcosα=a, o valor de a for tal que |a|>1, então o conjunto solução da equação é vazio.

Exemplo 2:

cosx = 2 ⇔ S = ∅

Exemplo 3: 

Exemplo 4:

O conjunto das soluções da equação sen 5x=cos3x contém o seguinte conjunto:

a) {^π/₁₆ + k ^π/₅ , k ∈ ℤ}
b) {^π/₁₆ + k ^π/₃ , k ∈ ℤ}
c) {^π/₄ + k ^π/₃ , k ∈ ℤ}
d) {^π/₄ + k ^π/₂ , k ∈ ℤ}
e) {^π/₄ + 2kπ , k ∈ ℤ}

Resolução: E

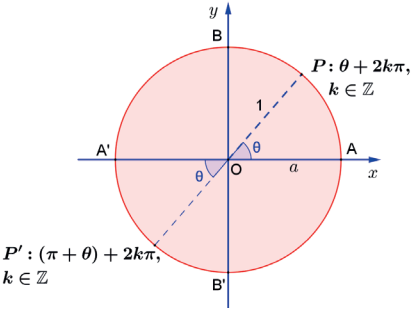
EQUAÇÃO EM TANGENTE

Seja a ∈ ℝ, então

tg α = a ⇔ α = arctg a + kπ, k ∈ ℤ

Observe que a equação em tangente possui solução para qualquer valor de a real.

A identificação das soluções da equação no ciclo trigonométrico encontra-se na figura seguinte.

Exemplo 1:

tg 2x = 1 ⇔ 2x = ^π/₄ + kπ, k ∈ ℤ ⇔ x = ^π/₈ + ^kπ/₂ , k ∈ ℤ

Exemplo 2: 

tg (4x – ^π/₄) = tg 2x ⇔ (4x – ^π/₄) – 2x = kπ, k ∈ ℤ ⇔ x = ^π/₈ + ^kπ/₂ , k ∈ ℤ