EQUAÇÃO REDUZIDA DA RETA
A reta r do gráfico a seguir é dada pela equação y = mx + n.
Coeficiente angular (declividade): o número real m.
Coeficiente linear: o número real n.
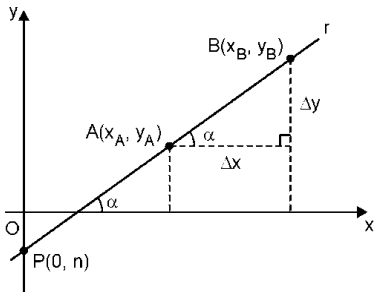
Interseção da reta r com o eixo Oy:
x = 0 ⇒ y = n ⇒ ponto P(0, n)
Propriedades do coeficiente angular:
m = tg a = Δx/Δy , onde Δx = xB − xA e Δy = yB − yA
Reta vertical: A equação de uma reta paralela ao eixo Oy é x = k, onde k é constante. Neste caso, não existem os coeficientes angular e linear.
Sabemos que para determinar uma reta é necessário, no mínimo, que tenhamos 2 pontos distintos ou também podemos determinar uma reta conhecendo um ponto e o ângulo formado pela reta e o eixo Ox↔.
É conhecido, desde o estudo da função afim, que uma reta é definida pela equação y = ax + b. Se conhecermos 2 pontos distintos A(xA, yA), B(xB, yB) podemos fazer:

Se utilizarmos as nomenclaturas utilizadas em geometria analítica a nossa equação será y = mx + n, sendo chamada de equação reduzida. Nessa equação teremos 2 elementos muito importantes.
m → Coeficiente angular
O coeficiente angular (m) será o responsável pelo ângulo formado pela reta e o eixo Ox↔. Como vimos o coeficiente angular será m = Δx/Δy , que ao olharmos para a figura abaixo veremos que Δx/Δy é a tangente do ângulo α.
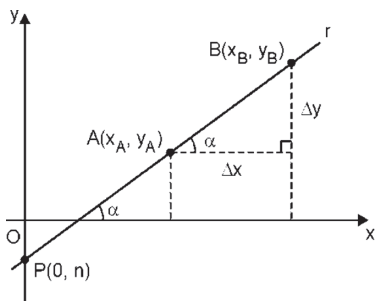
Logo m = tg α = Δx/Δy
n → Coeficiente linear
O coeficiente linear (n) será o responsável por determinar a intersecção da reta com e eixo Oy↔. Toda intersecção com o eixo Oy↔ se dá num ponto da forma (0,y).
Assim y = m ⋅ 0 + n ⇒ y = n, então o ponto de intersecção será (0,y).
Vamos ver um exemplo
Exemplo:
Encontrar equação de reta que passa pelos pontos A(2,1) e B(–3,4)
Sendo y = mx + n teremos m = 4−1/−3−2 = − 3/5
Assim nossa reta terá a equação y=− 3/5 x + n
Podemos usar o seguinte: (y– y0) = m(x– x0) onde x0 e y0 são as coordenadas de um ponto que pertença a reta.
Ou podemos também simplesmente substituir as coordenadas do ponto A ou do ponto B na equação y=− 3/5 x + n.

ProBizu: Tenha bastante atenção com pegadinhas que são colocadas. A reta só está na sua forma reduzida quando y está realmente isolado. Por exemplo 2y = x + 2 não tem seu m = 1 e n = 2 pois o y não está isolado na equação. Temos de fazer y = x+2/2 = x/2 + 1 para só assim determinarmos m = 1/2 e n=2. Atenção!
EQUAÇÃO DE RETA POR DETERMINANTE
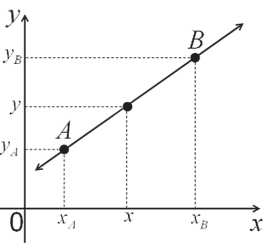
Introduzindo o ponto (x, y) na reta formada pelos pontos A e B teremos 3 pontos alinhados, onde vimos que a condição para estarem alinhados é

Exemplo: A equação de reta que passa pelos pontos A(2,1) e B(–3,4) é

INTERSECÇÃO DE DUAS RETAS
A teoria da intersecção entre duas retas é a mesma para quaisquer duas curvas, que é a resolução de um sistema entre as equações que representam cada uma das curvas.

A forma de resolução do sistema é a mesma da álgebra, podendo se dar pelo método da adição ou da substituição.
Exemplo: O ponto de intersecção entre as retas de equações y = x − 3 e 2y − 3x = 4 é





