EQUAÇÃO DE GAUSS
Podemos determinar a posição da imagem formada pelos espelhos e seu tamanho a partir da equação dos pontos conjugados ou equação de Gauss. Nós já vimos a abordagem gráfica, agora veremos o método analítico. Para isso, usaremos um sistema de coordenadas cartesianas (x, y) com origem no vértice do espelho. O eixo vertical será o próprio espelho e o eixo horizontal conterá o eixo principal e apontará para o lado de fora do espelho. Esse sistema é conhecido como referencial gaussiano e está representado abaixo:
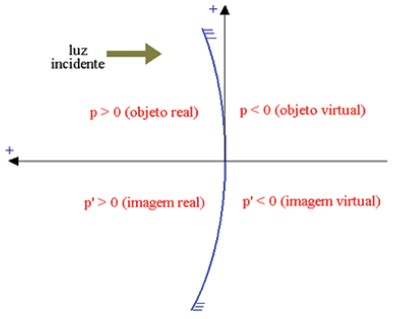
Referencial gaussiano para um espelho côncavo

em que,
- A posição dos objetos será representada por p.
- A posição das imagens será representada por p’.
- Elementos reais terão abscissa positiva.
- Elementos virtuais terão abscissa negativa e estarão dentro do espelho.
- A distância focal de um espelho côncavo tem abscissa positiva.
- A distância focal de um espelho convexo tem abscissa negativa.
AUMENTO LINEAR
Outra relação importante é o aumento linear, que quantifica quantas vezes o tamanho da imagem é maior (ou menor) que o do objeto.

- A > 0: a imagem e o objeto possuem o mesmo sinal, portanto a imagem é direita.
- A < 0: a imagem e o objeto possuem sinais contrários, portanto a imagem é invertida.
Exemplo: Um objeto encontra-se na frente de um espelho esférico de raio 12 cm. A imagem formada é direita e tem apenas 60% do tamanho do objeto. Qual a distância do objeto ao espelho?
Resolução: Se a imagem for menor que o objeto e é direita, sabemos que se trata de um espelho convexo e que a imagem é virtual, direita e menor (o espelho côncavo não produz imagem direita e menor).
Alerta-se: se a imagem for virtual, p’ é negativo (a imagem se forma atrás do espelho – sendo assim, pensando em eixos, p’ estaria na parte negativa) e, sendo um espelho convexo, a sua parte espelhada fica para fora; o foco aparece também atrás do espelho → espelho convexo tem foco negativo. Nesse caso, –6 cm (lembre-se de que o foco é a metade do raio).
Aplicando a relação de semelhança:

Se usássemos essa relação na equação de Gauss, erraríamos o problema. A relação acima é geométrica. Corrigindo o sinal (porque temos uma imagem virtual),
p’ = –0,6p.
Agora sim, substituindo na equação De Gauss:

Observação:

ASSOCIAÇÃO DE DOIS ESPELHOS
Vamos montar um banco óptico formado por dois espelhos esféricos onde as superfícies refletoras fiquem voltadas uma para outra e que os eixos principais coincidam.
Ao colocarmos um objeto luminoso entre os dois espelhos, obtém-se sua imagem em um deles e esta serve de objeto para o segundo espelho, fornecendo uma segunda imagem e assim sucessivamente. Com isso obtém-se um número muito grande de sucessivas imagens.
Vamos utilizar um exemplo.
Exemplo: Sobre um banco óptico são associados, coaxialmente, dois espelhos esféricos côncavos, de tal maneira que seus centros de curvatura sejam coincidentes. O espelho E1 tem raio de curvatura R1=12 cm e o E2 tem raio R2=18 cm. Um objeto frontal real O1 situa-se a 18 cm de E1. Localize a imagem fornecida por E2 ao receber os raios luminosos que emanam do objeto, incidem primeiramente em E1 e, após se refletirem nele, incidem em E2.
Resolução: Vamos montar o banco óptico.
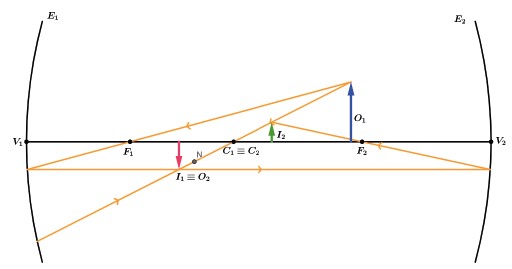
O1: objeto real para E1
IT: imagem real para E1
O2≡IT: objeto real para E2
I2: imagem real pedida
Vamos agora utilizar a equação de Gauss.

Estando a imagem I1 distante 9,0 cm de V1 estará a 3,0 cm de C1. No entanto, a imagem I1 será 0 objeto real O2 para o espelho E2.





