ELIPSE
A elipse é o lugar geométrico dos pontos plano cuja soma das distâncias a 2 pontos fixos (focos) é sempre constante e igual a 2a (eixo maior).
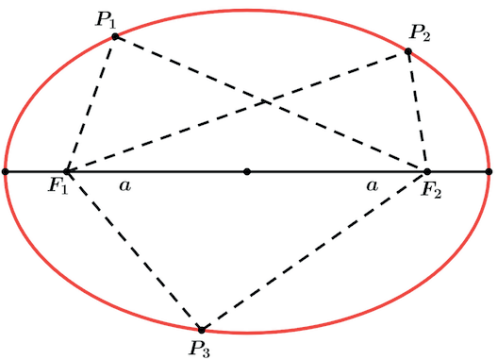
Sendo assim, ao escolhermos qualquer ponto que esteja sobre a elipse, por exemplo P1, ao traçarmos a distância de P1 a um dos focos e a distância de P1 ao outro foco e somarmos essas distâncias encontraremos sempre o mesmo valor 2a, que é exatamente o valor do eixo maior da elipse.

ELEMENTOS DA ELIPSE
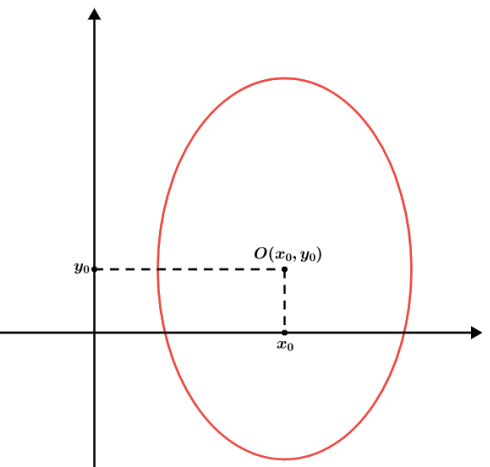
Toda elipse possui um centro que chamaremos de (x0, y0), paralelos aos eixos Ox↔ e Oy↔ passando pelo centro (x0, y0) teremos o eixo maior A̲1̲A̲2̲, no mesmo segmento de reta a distância focal e no segmento de reta perpendicular o eixo menor B̲1̲B̲2̲.
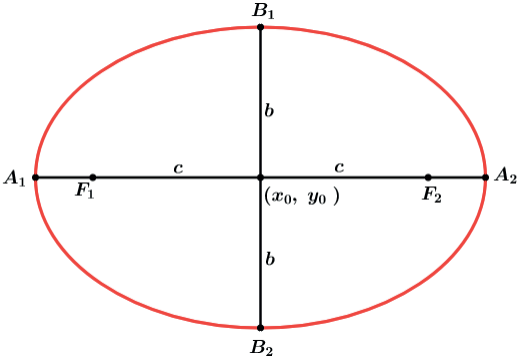
Observação, também podemos ter a elipse “de pé”, falaremos mais sobre ela mais a frente.
A̲1̲A̲2̲ → Eixo maior, representado 2a.
B̲1̲B̲2̲ → Eixo menor, representado por 2b.
F̲1̲F̲2̲ → Distância focal, representada por 2c.
Perceba que na elipse deitada esse será o funcionamento a partir do centro (x0,y0).
A1 = x0 – a
A2 = x0 + a
B1 = y0 + b
B2 = y0 – b
F1 = x0 – c
F2 = x0 + c
Na elipse em pé
A1 = y0 – a
A2 = y0 + a
B1 = x0 + b
B2 = x0 – b
F1 = y0 – c
F2 = y0 + c
RELAÇÃO FUNDAMENTAL DA ELIPSE
Utilizando a propriedade da elipse como lugar geométrico.
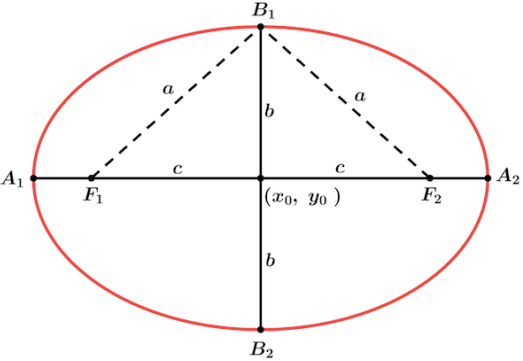
Considerando o ponto B1 teremos que B̲1̲F̲1̲ + B̲1̲F̲2̲ = 2a, porém o triângulo F1B1F2 é isósceles, F̲1̲O̲ = F̲2̲O̲ e A̲1̲A̲2 ⊥ B̲1̲B̲2̲.
Observação: O = centro (x0, y0) da elipse.
Assim com o triângulo F1B1F2 sendo isósceles teremos B̲1̲F̲1̲ = B̲1̲F̲2̲ ⇒ B̲1̲F̲1̲ = B̲1̲F̲2̲ = a. Daí podemos aplicar o teorema de Pitágoras no triângulo retângulo encontrando a relação fundamental da elipse.
a² = b² + c²
EQUAÇÃO FUNDAMENTAL DA ELIPSE
Fazendo a elipse com centro em (0, 0) de um eixo cartesiano transladado e aplicando que P̲1̲F̲1̲ + P̲1̲F̲2 = 2a, onde o ponto P1 =(x, y) é um ponto qualquer do plano, teremos:

Essa é a equação da elipse de eixo maior horizontal:

percebemos que o valor a (o maior valor), irá “aparecer” no denominador de x.
A equação da elipse de eixo maior vertical:

O valor a (o maior valor), irá “aparecer” no denominador de y.
EQUAÇÃO COMPLETA
Temos por exemplo a equação da elipse (x−2)²/9 + (y−1)²/4 = 1 de onde podemos perceber que possui o centro em (2, 1) e a² = 9 ⇒ a = 3 e b² = 4 ⇒ b = 2. Assim vemos que é uma elipse horizontal onde o eixo maior mede 6 e o eixo menor mede 4. Vamos desenvolver a equação.

Assim ficamos com a equação 4x² + 9y² − 16x −18y −11 = 0 que da forma que está não conseguimos identificar as coordenadas do centro ou os valores de a e de b.
Para chegarmos novamente a equação reduzida deveremos usar o mesmo artifício que utilizamos na equação da circunferência, completar quadrados.

Assim teríamos:
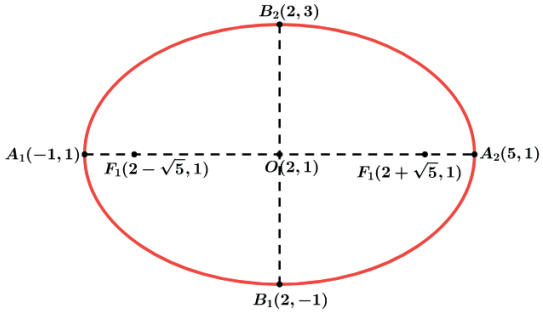
O(2, 1)
A1(−1, −1)
A2(5, −1)
B1(2, −1)
B2(2, 3)
F1(2 − √5, 1)
F2(2 + √5, 1)
Lembrando:
- Elipse centrada na origem com eixo maior paralelo ao eixo x.
x²/a² + y²/b² = 1
- Elipse centrada na origem com eixo maior paralelo ao eixo y.
x²/b² + y²/a² = 1
Para você que gosta de fórmulas, vamos tentar comprimir a equação completa de forma totalmente literal.

Parece complicado? Mas encontramos o centro de maneira rápida, vamos ver com o exemplo anterior.





