Elipse

DEFINIÇÃO GERAL DAS CÔNICAS

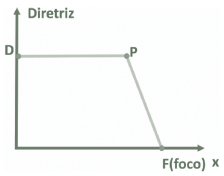
Cônica é o lugar geométrico dos pontos de um plano cuja razão entre as distâncias a um ponto fixo F (foco) e a uma reta fixa d (diretriz) é igual a uma constante não negativa e (excentricidade da cônica). A excentricidade “e” é um número não negativo, pois é a razão de duas distâncias.

Se e = 1, a cônica é uma parábola.
Se 0 < e < 1, a cônica é uma elipse.
Se e > 1, a cônica é uma hipérbole.

ELIPSE

Dados dois pontos fixos F₁ e F₂ de um plano, tais que, F₂F₁ = 2c ≠ 0, chamamos elipse ao lugar geométrico dos pontos deste plano, cuja soma das suas distâncias aos dois pontos F₂ e F₁ é constante igual a 2a > 2c.

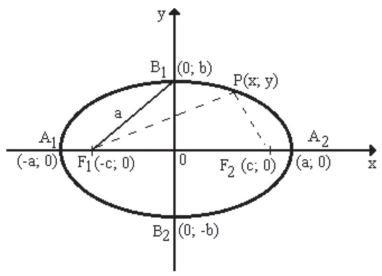
ELEMENTOS DA ELIPSE

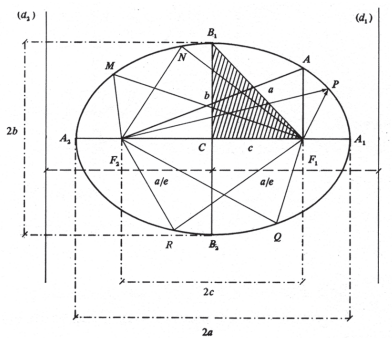
I. PONTOS PRINCIPAIS:

A₂, A₁, B₂, B₁ – vértices
F₂ e F₁ – focos
C – centro

II. SEGMENTO:

A₂A₁ – eixo maior – m(A₂A₁) = 2a
B₂B₁ – eixo menor – m(B₂B₁) = 2b
F₂F₁ – distância focal – m(F₂F₁) = 2c

III. RELAÇÕES:

“Parâmetro de uma cônica é a semicorda focal mínima.”

IV. RETAS – DIRETRIZES:

Diretrizes da elipse são duas retas, (D₁) e (d₂), perpendiculares ao suporte do eixo maior, distando ^a/_e do centro da curva.

EQUAÇÃO REDUZIDA

EIXO MAIOR NO EIXO X

As equações das diretrizes são x = ± ^a/_e

ELIPSE “DE PÉ”

Se F₁(0,C) e F₂(0,−C), o eixo maior está sobre o eixo y

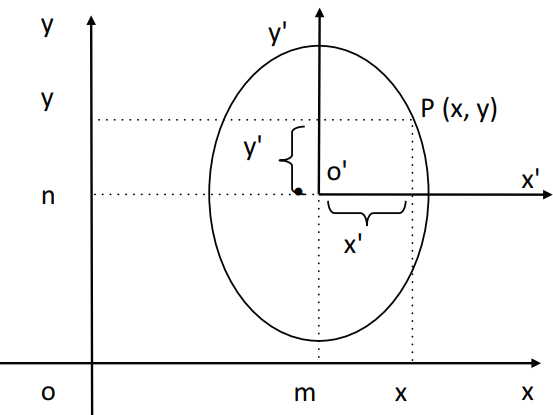
EQUAÇÃO DA ELIPSE QUANDO HÁ TRANSLAÇÃO DE SISTEMA

1° caso: elipse com centro O(m,n) e eixo maior horizontal.

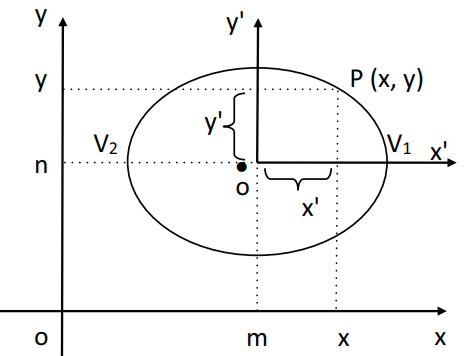
2° caso: elipse com centro O(m,n) e eixo maior vertical.

POSIÇÕES RELATIVAS ENTRE PONTO E ELIPSE

Sejam εε uma elipse de focos F₁ e F₂, cujo eixo maior mede 2a, e P um ponto do ponto do plano de ε.

1° caso: A é ponto da elipse.
A pertence à elipse εε se, e somente se PF₁ + PF₂ = 2a
2° caso: A é interior à elipse ε. PF₁ + PF₂ < 2a
3° caso: A é exterior à elipse ε. PF₁ + PF₂ > 2a

PROCESSO PRÁTICO:

A quantidade de pontos de interseção entre a reta r e a elipse ∩ε é dada pelo número de soluções do sistema formado pelas equações de r e ε, resolvido substituindo-se uma variável previamente isolada na equação de r na equação de ε. Com isso, se:

I. ∆ > 0: r é secante a ε;
II. ∆ = 0: r é tangente a ε;
III. ∆ < 0: r é exterior a ε.