Podem ser de vários formatos: cilíndricos, esféricos, planos, etc.

Capacitores
Disponível em: http://blog.perautomacao.com.br
CAPACITÂNCIA
A capacidade que os capacitores tem de armazenar carga é denominada capacitância, simbolizada por C, cuja unidade SI é o farad (F). Esse valor depende das características geométricas do corpo (forma e tamanho) bem como do material dielétrico no seu interior, como veremos mais adiante.
A carga (Q) adquirida pelo capacitor está atrelada à ddp (U) na qual ele for conectado. Assim podemos definir a capacitância como:

Observação: 1F é um valor muito grande, por isso utilizamos submúltiplos do farad:
- mF =10-3 F
- μF =10-6 F
- nF =10-9 F
Vamos agora calcular a capacitância para as duas principais formas de capacitores: esférico e plano.
CAPACITOR ESFÉRICO
Lembrando das aulas de potencial elétrico, o potencial na superfície de uma esfera carregada de raio R vale

Assim a sua capacitância é dada por:

Observe que a capacitância é diretamente proporcional ao raio da esfera.
CAPACITOR PLANO DE PLACAS PARALELAS
Esse capacitor será a principal representação desses componentes nos circuitos elétricos.
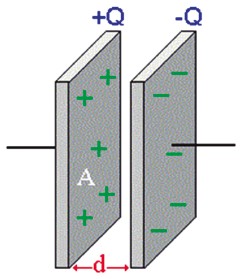
Capacitor plano de placas paralelas
A capacitância desse capacitor vale:

Em que:
ε0 é a permissividade elétrica do vácuo
A é a área da seção das placas
d é a distância entre as placas
DIELÉTRICOS
Dielétrico é um material isolante que será colocado entre as armaduras de um capacitor a fim de aumentar sua capacitância. Isso ocorre pelo aumento da permessividade elétrica do meio para um novo valor ε > ε0.
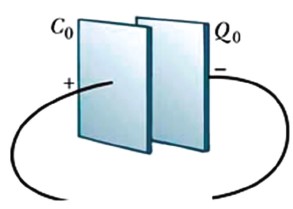
Capacitor isolado à vácuo
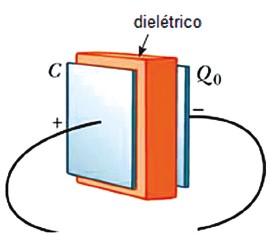
Capacitor preenchido por um dielétrico
Vamos definir um valor κ chamada de permissividade relativa, que só depende da composição do dielétrico cujo valor será a razão entre as permissividades elétricas com e sem o dielétrico, ou seja:

Dessa maneira, a nova capacitância será dada por:

Observação: Como funciona o dielétrico?
Mesmo sendo um material isolante, o dielétrico ainda é polarizado pelas cargas nas armaduras do capacitor original. Isso reduz o campo elétrico no seu interior, permitindo que mais cargas passem para o capacitor, aumentando sua carga e energia armazenada.
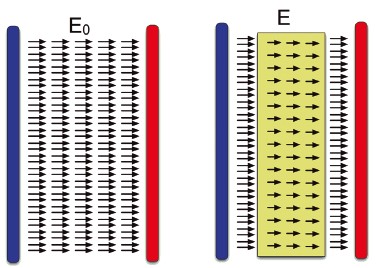
O campo elétrico em um capacitor sem e com dielétrico
ENERGIA DE UM CAPACITOR
A energia armazenada pelo capacitor (E) pode ser calculada a partir do gráfico da carga pela tensão. Lembrando que a área sob o gráfico Q × U fornecerá a energia potencial elétrica.
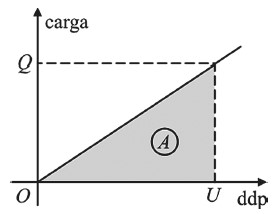
Gráfico da carga pela ddp em um capacitor

Usando a relação entre a carga e a capacitância, podemos escrever três equações equivalentes para o cálculo da energia armazenada no capacitor.

CARREGANDO UM CAPACITOR
A bateria quando conectada a um capacitor fará com que os elétrons fluam devido à ddp gerada. Depois de algum tempo, no entanto, o capacitor já possuirá tantas cargas que não conseguirá mais ser carregado. Dizemos que ele atingiu o estado estacionário, ou seja, está completamente carregado.
Representação de um capacitor em um circuito
Estudaremos somente os capacitores nesse regime estacionário, sem nos preocuparmos com o processo que o levou até esse estágio.
A ddp no capacitor será igual à da bateria na qual ele está ligado, isto é, Ucapacitor = Ubateria =U e sua carga será dada pela expressão:
Q = C · U
Observação: O tempo para atingir o regime estacionário é de alguns milissegundos, por isso podemos trabalhar com o circuito já no equilíbrio. A partir desse instante, não há corrente circulando pelo capacitor e podemos representá-lo como um circuito aberto.
ASSOCIAÇÃO DE CAPACITORES
Os capacitores, assim como resistores e geradores, podem ser associados em série ou em paralelo num circuito elétrico. Vejamos as características de cada associação:
SÉRIE
Capacitores em série compartilham a mesma carga, porém a tensão é dividida.
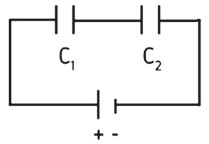
Capacitores ligados em série
Para determinarmos a carga e a tensão de cada capacitor, convém substitui-los por um único capacitor equivalente, cuja carga será a mesma dos capacitores que o compõem e a diferença de potencial será igual à da bateria na qual eles estão ligados.
Q = Q1 = Q2U = U1 + U2
Dessa forma, lembrando que U = Q/C

Observe que a fórmula para capacitores associados em série é a mesma para resistores em paralelo.
Não confunda!
- Para dois capacitores, a equação se reduz a:

- Para N capacitores iguais a C, a equação assume a forma de:

PARALELO
Capacitores em série possuem a mesma tensão.
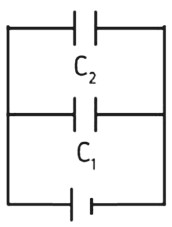
Capacitores ligados em paralelo
Podemos determinar a capacitância equivalente, cuja carga será a soma das cargas de cada capacitor do circuito
Q = Q1 + Q2U = U1 = U2
Dessa forma, lembrando que Q = C · U
Q = Q1 + Q2 ⇒ Ceq · U = C1 · U1 + C2 · U2Ceq = C1 + C2
Observação: Observe que a fórmula para capacitores associados em paralelo é a mesma para resistores em série. Não confunda!




