Ao analisar as cargas elétricas, a força magnética passa a existir quando uma partícula eletricamente carregada movimenta-se em uma região onde atua um campo magnético.
Considerando que uma carga pontual q, com velocidade v, seja lançada em uma região onde existe um campo magnético uniforme B, passa a atuar sobre ela uma força magnética com intensidade dada pela seguinte equação:
F = |q| · v × B · sen θ
*θ é o ângulo entre os vetores da velocidade v e do campo magnético B.
A direção do campo magnético é perpendicular ao plano que contém os vetores v e F, e o sentido é dado pela regra da mão direita.
A regra da mão direita diz o seguinte: o dedo polegar deve ser colocado sempre no sentido da velocidade v, os outros quatros dedos parados devem sempre ser colocados no sentido do campo magnético B, finalmente a força magnética terá o sentido da sua palma da mão como se você estivesse empurrando a palma da sua mão. Nesse caso, a regra da mão direita é também conhecida como regra do tapa.
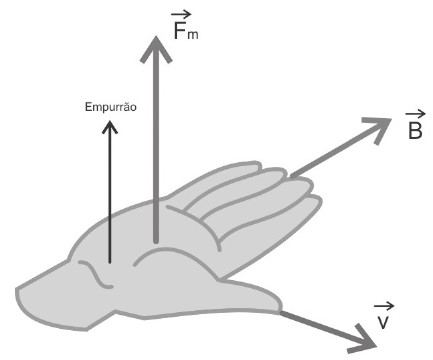
Disponível em: http://3.bp.blogspot.com/_JJJ4o4Jcg48/TNg9EC8_BCI/AAAAAAAAYHk/reYYMYox-7k/s1600/maozinha+11.jpg
EFEITOS DE UM CAMPO MAGNÉTICO SOBRE CARGA
CARGA ELÉTRICA EM REPOUSO
“Um campo magnético estacionário não interage com cargas em repouso.”
Tendo um Ímã posto sobre um referencial arbitrário R, se uma partícula com carga q for abandonada em sua vizinhança com velocidade nula não será observado o surgimento de força magnética sobre esta partícula, sendo ela positiva, negativa ou neutra.
CARGA ELÉTRICA COM VELOCIDADE NA MESMA DIREÇÃO DO CAMPO
“Um campo magnético estacionário não interage com cargas que tem velocidade não nula na mesma direção do campo magnético.”
Sempre que uma carga se movimenta na mesma direção do campo magnético, sendo no seu sentido ou contrário, não há aparecimento de força eletromagnética que atue sobre ela. Um exemplo deste movimento é uma carga que se movimenta entre os polos de um Ímã. A validade desta afirmação é assegurada independentemente do sinal da carga estudada.
Observe que, nesse caso, o ângulo θ = 0º ou θ = 180 º. A equação que utilizamos para calcular a força é:
F = |q| · v · B · sen θ
E o sen 0º = sen 180º = 0
Substituindo na equação, teremos:
F = |q| · v · B · 0
F = 0
Se a força é igual a zero, a partícula mantém-se com a mesma velocidade e realiza movimento retilíneo uniforme na mesma direção do campo magnético.
CARGA COM MOVIMENTO PERPENDICULAR AO CAMPO
Uma partícula eletrizada com carga elétrica q é lançada perpendicularmente às linhas de indução, isto é, v é perpendicular a B. Nesse caso, θ = 90°. Nessa situação, como θ = 90°, a força magnética Fmg age como uma força centrípeta, modificando apenas a direção da velocidade v da partícula de carga elétrica q, sem provocar variações em seu módulo. Desse modo, essa partícula passa a descrever no interior do campo magnético um movimento circular uniforme.
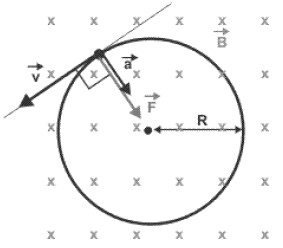
Disponível em: http://www.alfaconnection.pro.br/images/MAG020105a.gif
Com isso, temos:
o ângulo entre v e B será θ = 90º. Como sen 90º = 1, teremos:
F = |q| · v · B · sen 90
F = |q| · v · B · 1
F = |q| · v · B
O movimento executado pela partícula é circular e uniforme, e o raio de sua trajetória é obtido da seguinte forma:
F = Fcp
Sabemos que:

Igualamos as expressões e obtemos:

Quanto maior for a massa da partícula, maior será o raio de sua trajetória.
TRAJETÓRIAS HELICOIDAIS
Se a velocidade de uma partícula carregada tem uma componente paralela ao campo magnético (uniforme), a partícula descreve uma trajetória helicoidal cujo eixo é a direção do campo.
A componente paralela dá origem a um movimento de transição e a perpendicular origina um movimento circular uniforme (rotação). Quando há sobreposição dessas duas componentes gera uma trajetória helicoidal, em forma de hélice.
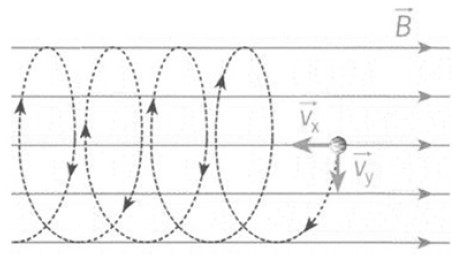
Disponível em: http://alunosonline.uol.com.br/upload/conteudo/images/helice-cilindrica.jpg
FORÇA MAGNÉTICA SOBRE UM FIO CONDUTOR
Sempre que uma carga é posta sobre influência de um campo magnético, esta sofre uma interação que pode alterar seu movimento. Se o campo magnético em questão for uniforme, vimos que haverá uma força agindo sobre a carga com intensidade FM = |q| v B senθ, onde θ é o ângulo formado no plano entre os vetores velocidade e campo magnético. A direção e sentido do vetor FM→ serão dadas pela regra da mão direita.
Se imaginarmos um fio condutor percorrido por corrente, haverá elétrons livres se movimentando por sua secção transversal com uma velocidade v→. No entanto, o sentido adotado para o vetor velocidade, neste caso, é o sentido real da corrente (v→ tem o mesmo sentido da corrente). Para facilitar a compreensão pode-se imaginar que os elétrons livres são cargas positivas.
Como todos os elétrons livres têm carga (que pela suposição adotada se comporta como se esta fosse positiva), quando o fio condutor é exposto a um campo magnético uniforme, cada elétron sofrerá ação de uma força magnética.
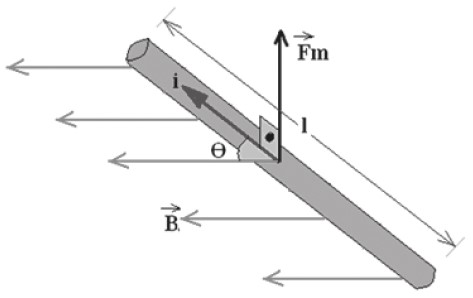
Disponível em: http://alunosonline.uol.com.br/upload/conteudo/images/for%C3%A7a%20mag1.gif
Mas se considerarmos um pequeno pedaço do fio ao invés de apenas um elétron, podemos dizer que a interação continuará sendo regida por FM = |q| v B senθ, onde Q é a carga total no segmento do fio, mas como temos um comprimento percorrido por cada elétron em um determinado intervalo de tempo, então podemos escrever a velocidade como:

Ao substituirmos este valor em FM→ teremos a força magnética no segmento, expressa pela notação :

Mas sabemos que |Q|/Δt indica a intensidade de corrente no fio, então:

Sendo esta expressão chamada de Lei Elementar de Laplace.
A direção e o sentido do vetor fM→ são perpendiculares ao plano determinado pelos vetores v→ e B→, e pode ser determinada pela regra da mão direita espalmada, apontando-se o polegar no sentido da corrente e os demais dedos no sentido do vetor B→.
FORÇA MAGNÉTICA ENTRE FIOS PARALELOS
Ampère fez estudos relacionados à força magnética produzida entre dois fios conduzidos por energia elétrica. Em seus estudos, ele conseguiu determinar a intensidade do campo magnético produzido por tal corrente elétrica. A força magnética entre dois fios paralelos e separados por uma distância d pode ser determinada da seguinte maneira:
Inicialmente devemos fazer os cálculos da intensidade do campo magnético B1 na posição do fio 2. Dessa forma, o campo produzido pela corrente i1 vale:

Em seguida podemos efetuar os cálculos do módulo da força magnética que atua sobre o fio 2 através da seguinte equação: F1 = B1 · i2 · L. Nessa equação, L é o comprimento do fio. Dessa forma, podemos ver que a força magnética que atua no fio 2 é dada pela seguinte relação:
no vácuo temos que µ = 4π · 10-7 T ⋅ m/A.
De tal modo, podemos dizer que o mesmo efeito ocorre para o campo magnético gerado pelo fio 2. Assim, o campo magnético criado pela corrente i2 na posição do fio 1 também produz uma força sobre a corrente i1. A força tem a mesma intensidade que a força F2, mas tem sentido contrário. Essas duas forças formam um par de ação e reação.
Utilizando a regra da mão direita podemos ver que se as correntes estiverem no mesmo sentido, a força magnética entre os fios será de atração. Caso as correntes possuam sentidos contrários, a força será de repulsão entre os fios.
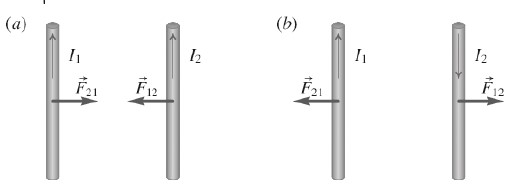
Disponível em: https://def.fe.up.pt/eletricidade/img/forca_magnetica_fios_560.png




