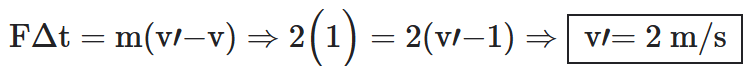IMPULSO
A ideia de impulso se apresenta para nós usualmente como um empurrão cujo objetivo é acelerar ou freiar um objeto. Essa aceleração dependerá da força (F→) a ser aplicada e do seu tempo (∆t) de interação com o corpo, assim, o impulso (I→) será definido como:
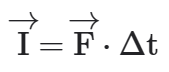
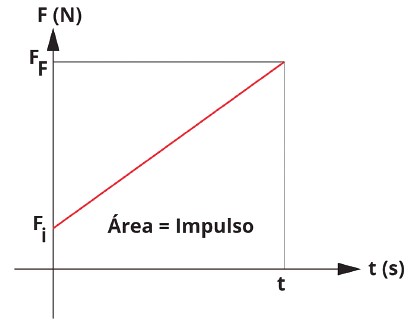
Observação: Quando a força for variável, podemos usar a área do gráfico F × t para determinar o valor do impulso.
Observação: No SI, o impulso é dado em N ⋅ s
QUANTIDADE DE MOVIMENTO
A quantidade de movimento (Q→) é a grandeza utilizada por Newton para formulação das leis da mecânica. Também chamada de momento linear, é definida pelo produto da massa (m) de um corpo pela sua velocidade (v→).
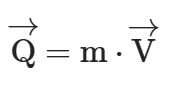
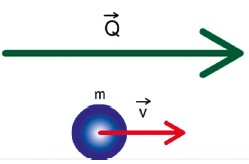
Observação: No SI, a unidade de quantidade de movimento é kg ⋅ m/s
Exercício Resolvido 1: Em uma aula do curso de Logística Aeroportuária, o professor propõe aos alunos que determinem a quantidade de movimento da aeronave tipo 737-800 em voo de cruzeiro, considerando condições ideais. Para isso ele apresenta valores aproximados, fornecidos pelo fabricante da aeronave.

om base nos dados apresentados no quadro, o resultado aproximado esperado é, em kg ⋅ m/s,
a) 1,6 × 107
b) 2,0 × 107
c) 2,6 × 107
d) 3,0 × 107
e) 3,6 × 107
Resolução: A
A quantidade de movimento ou momento linear (Q) é o produto da massa pela velocidade, assim para a velocidade de cruzeiro, em m/s, temos:
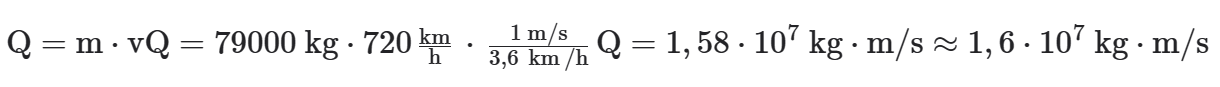
Observação: Há uma relação entre a energia cinética do corpo e sua quantidade de movimento dada por:
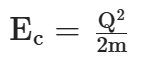
TEOREMA DO IMPULSO
A segunda lei de Newton pode ser escrita em função das grandezas apresentadas nesse capítulo, como veremos a seguir:
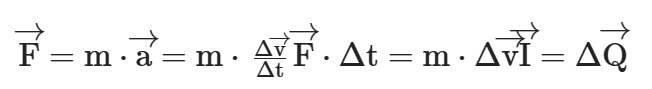
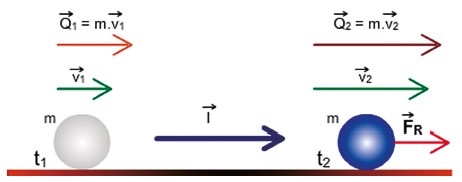
Assim, quando uma força resultante é aplicada em um corpo, ela provoca uma variação na sua quantidade de movimento.
Exercício Resolvido 2: Uma partícula de massa m2 = 2 kg está em movimento retilíneo sobre uma superfície sem atrito com velocidade constante v = 1 m/s. Ao se fazer atuar sobre a partícula uma força constante de módulo F = 2 N na mesma direção e no mesmo sentido de seu movimento, durante um intervalo ∆t = 1 s, ela sofre uma aceleração constante. Ao final do intervalo de tempo ∆t = 1s a velocidade da partícula, em m/s, será
a) 0.
b) 1.
c) 3.
d) 4.
e) 2.
Resolução: E
Sendo a força aplicada a resultante, aplicando o teorema do impulso: