Dinâmica: Colisões

Quando dois ou mais corpos colidem, eles interagem entre si e causam variação das suas quantidades de movimentos.

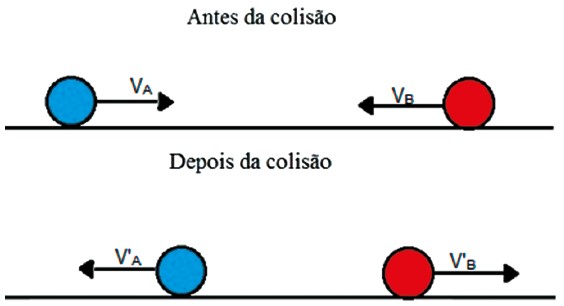
Não havendo forças externas atuando, a quantidade de movimento do sistema de partículas permanece sempre inalterado.

Observação: Em quaisquer colisões a quantidade de movimento do sistema sempre é conservada.

Demonstração da conservação da quantidade de movimento

Usando a terceira lei de Newton (ação e reação), podemos afirmar que a força (F_AB→) que o corpo A faz em B é oposta a que B faz em A (F_BA→). Além disso, o tempo de interação entre eles também é o mesmo, assim:

Usando o teorema do impulso, temos:

OEFICIENTE DE RESTITUIÇÃO

Mesmo com a quantidade de movimento total conservada, a energia dos corpos após uma colisão pode não se manter constante. Para determinarmos quanto da energia é perdida nesse processo, usaremos o coeficiente de restituição (e) definido por:

v_{aproximação} é a velocidade relativa entre os corpos antes da colisão.
v_afastamento é a velocidade relativa entre os corpos após a colisão.

Observação: Relembrando como calcular a velocidade relativa

Corpos se movendo no mesmo sentido: v_rel = |v₁ – v₂|
Corpos se movendo em sentido contrário: v_rel = |v₁ + v₂|

COLISÃO PERFEITAMENTE ELÁSTICA

Vamos descrever as características de uma colisão perfeitamente elástica e fazer um exemplo:

não há perda de energia, ou seja, a energia é conservada.
o coeficiente de restituição vale 1 (e = 1).

Exercício Resolvido 1: Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso no ponto A, é largado de uma altura h = 0,8 m. O bloco desliza ao longo de uma superfície sem atrito e colide com um outro bloco, de mesma massa, inicialmente em repouso no ponto B (veja a figura a seguir). Determine a velocidade do segundo bloco após a colisão, em m/s, considerando-a perfeitamente elástica.

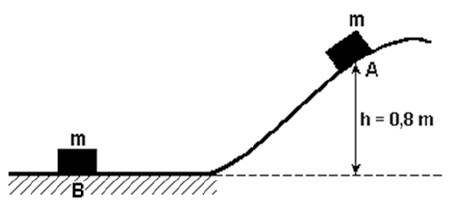
Resolução:

Primeiro vamos encontrar a velocidade do bloco A no final da rampa usando a conservação da energia

Durante colisão, a quantidade de movimento é conservada

Como a colisão é perfeitamente elástica, o coeficiente de restituição vale 1

Resolvendo o sistema, encontramos:

Pêndulo de Newton

COLISÃO PERFEITAMENTE INELÁSTICA

Vamos também descrever as características de uma colisão perfeitamente inelástica e fazer um exemplo:

A energia não é conservada.
Há perda máxima de energia do sistema.
Os corpos saem juntos após a colisão.
O coeficiente de restituição é nulo (e = 0).

Exercício Resolvido 2: Um corpo A colide com um corpo B que se encontra inicialmente em repouso. Os dois corpos estão sobre uma superfície horizontal sem atrito. Após a colisão, os corpos saem unidos, com uma velocidade igual a 20% daquela inicial do corpo A.

Qual é a razão entre a massa do corpo A e a massa do corpo B, m_A/m_B?

a) 0,20

b) 0,25

c) 0,80

d) 1,0

e) 4,0

Resolução: B

A colisão entre os dois corpos é perfeitamente inelástica sem atrito, assim temos a Conservação da Quantidade de Movimento.

COLISÃO PARCIALMENTE ELÁSTICA OU PARCIALMENTE INELÁSTICA

Essas colisões são intermediárias entre a perfeitamente elástica e a perfeitamente inelástica, portanto o seu coeficiente de restituição está entre 0 e 1 (0 < e < 1). Sua energia também não é conservada.

Exercício Resolvido 3: (EFOMMM) Dois móveis P e T com massas de 15,0 kg e 13,0 kg respectivamente, movem-se em sentidos opostos com velocidades V_P = 5,0 m/s e V_T = 3,0 m/s, até sofrerem uma colisão unidimensional, parcialmente elástica de coeficiente de restituição e = 3/4. Determine a intensidade de suas velocidades após o choque.

a) V_T = 5,0 m/s e V_P = 3,0 m/s

b) V_T = 4,5 m/s e V_P = 1,5 m/s

c) V_T = 3,0 m/s e V_P = 1,5 m/s

d) V_T = 1,5 m/s e V_P = 4,5 m/s

e) V_T = 1,5 m/s e V_P = 3,0 m/s

Resolução: B

Orientando a trajetória no mesmo sentido do movimento do móvel P, os dados são: m_P = 15 kg; m_T =13 kg; v_P = 5 m/s; v_T = -3 m/s.

Considerando o sistema mecanicamente isolado, pela conservação da quantidade de movimento: