Os efeitos associados a esse fenômeno geralmente não são percebidos por nós, mas são levados em consideração na hora de montar uma ferrovia, por exemplo. As barras dos trilhos ferroviários são feitas com um espaçamento para não envergarem com o aumento da temperatura, ou retraírem com a sua queda. O estudo da dilatação é dividido em três partes: Quando uma das dimensões é muito maior que as demais, a dilatação ocorre praticamente apenas em uma dimensão, chamada de dilatação linear (o exemplo das barras dos trilhos está dentro desse tipo de dilatação). Quando duas dimensões são bem maiores que a outra, a dilatação ocorrerá quase que totalmente nessas dimensões, chamada de dilatação superficial (uma chapa de metal, ao ser aquecida, expande-se bidimensionalmente).
Quando estamos falando de um líquido/gás, a dilatação será volumétrica, ou seja, nas três dimensões. Em sólidos, cujos comprimentos das três dimensões são próximos/iguais, também ocorrerá a dilatação volumétrica. Cada material se expande de maneira única. Dizemos que cada elemento tem o seu próprio coe ciente de dilatação. Geralmente, quando falamos de sólidos, iremos usar metais nos problemas, já que, nesse tipo de material, ocorre uma boa condução de calor, sendo então, melhor observado o fenômeno. Outro fator importante para medirmos o quanto dilatará certo material é o seu comprimento/ área/volume inicial. Quanto maior for, maior será sua dilatação. Por exemplo, um pedaço de ferro de 1 cm crescerá menos que outro de 1 m, se submetidos a mesma variação de temperatura. O último fator a ser analisado justamente é a variação de temperatura. Quanto maior a variação, maior será a alteração da(s) dimensão(ões) do material.
DILATAÇÃO LINEAR DOS SÓLIDOS
Através de experiências é possível verificar que a variação do comprimento de uma barra (∆L) depende do seu comprimento inicial (L0) e da variação de temperatura que ela sofre (∆T).

A constante de proporcionalidade α que comparece nessa equação, que traduz a lei da dilatação linear, é denominada coeficiente de dilatação linear do material.
UNIDADE DO COEFICIENTE DE DILATAÇÃO LINEAR
Se isolarmos a na equação ∆L = α · L0 · ∆T teremos:

Como ∆L e L0 tem a mesma unidade teremos que a unidade de a será o inverso da temperatura onde muitas vezes será usado o ºC-1 e no SI o K-1.
CÁLCULO DO COMPRIMENTO FINAL
Não podemos esquecer que ∆L é apenas a dilatação e que dessa forma o comprimento final será o comprimento inicial L0 mais a dilatação ∆L e assim:

Exemplo: Uma régua de 1m feita de alumínio, cujo coeficiente de dilatação linear vale 25·10-6 C-1, sofre um aumento de 70ºC. Qual foi a dilatação sofrida?
Resolução:
Como a régua apresenta uma dimensão bem superior as demais, trata-se de uma dilatação linear. E, como o coeficiente é menor que 10-3 °C-1, podemos usar a aproximação acima:

Note que a dilatação é muito pequena (0,175%).
DILATAÇÃO SUPERFICIAL DOS SÓLIDOS
Imagine que temos uma chapa metálica retangular a x b. Como a dilatação ocorrerá nas duas dimensões, usando a aproximação acima, teremos:

Em que A é a área final e A0 a área inicial.

O termo a²(∆T)² é muito, mas muito pequeno e assim

Podemos escrever como:

Em que β = 2α, chamado de coeficiente de dilatação superficial.
Exemplo: Uma chapa quadrada de 20 cm de lado de alumínio sofreu um aquecimento de 600 K. Qual é a dilatação superficial sofrida pela chapa?
Resolução:

Uma variação percentual de 3% (com um aumento de 600 K).
DILATAÇÃO VOLUMÉTRICA DOS SÓLIDOS
A variação do volume de um corpo sólido também é analisada a partir da dilatação de cada uma das dimensões lineares do corpo.
Imagine um paralelepípedo retângulo de dimensões iniciais iguais a x0, y0 e z0 com volume inicial v0 = x0 · y0 · z0. Assim a dilatação linear para cada dimensão será

Assim o novo volume do paralelepípedo será

Da mesma maneira quando fizermos (1 + α · ΔT)³ poderemos aproximar para

Sendo assim

Chamamos coeficiente de dilatação cúbica ou volumétrica do material do corpo o termo 3α, indicando-o por γ.

VARIAÇÃO DA DENSIDADE COM A TEMPERATURA
Vamos considerar a densidade inicial de um corpo como d0 = m/V0 e a densidade final desse corpo, após uma dilatação, de d = m/V

DILATAÇÃO TÉRMICA DOS LÍQUIDOS
Os líquidos não têm forma própria e assim adquirem a forma do recipiente em que estão sendo assim, o volume de líquido é o volume do recipiente em que ele está contido. De modo geral, os líquidos se dilatam mais que os sólidos. Por isso, se um recipiente estiver cheio de líquido até a borda, um aumento na temperatura acarreta transbordamento do líquido.
DILATAÇÃO APARENTE
Quando vamos medir a dilatação de um líquido devemos levar em consideração a dilatação do recipiente em que o líquido está contido e dessa forma tem suas dimensões alteradas. Quando isso acontece temos o que chamamos de dilatação aparente dos líquidos.
Vamos imaginar um líquido dentro de um recipiente estando este recipiente cheio até a borda, ou seja, completamente cheio. Ao aquecermos o recipiente e o líquido vamos supor que parte do líquido derrama. O líquido extravasado não representa toda a dilatação do líquido uma vez que o recipiente também dilatou sendo assim o líquido extravasado será o volume aparente.
Para determinação do volume aparente utilizaremos o coeficiente de dilatação aparente
γap = γ – γs
γap → coeficiente de dilatação aparente
γ → coeficiente de dilatação real
γs → coeficiente de dilatação do recipiente
A variação de volume aparente ∆Vap será a diferença entre o volume derramado e o volume inicial.

Onde também teremos:

Exemplo: Consideremos um frasco de vidro graduado em cm³ a 15 ºC. Dentro desse frasco coloca-se um líquido a 15 ºC, até atingir a marca de 500 cm³. A seguir, aquece-se o conjunto até 95 ºC e observasse que o líquido atinge a marca de 506 cm³.
Sabendo que o coeficiente de dilatação cúbica do vidro é 27 · 10 ⁻⁸°C-1, calcule:
a) a variação aparente de volume do líquido;
b) o coeficiente de dilatação cúbica aparente do líquido;
c) o coeficiente de dilatação cúbica real do líquido;
d) o volume real de líquido a 95 ºC.
Resolução:

COMPORTAMENTO ANÔMALO DA ÁGUA
Contrariamente a maioria das substâncias a água possui um comportamento anômalo quando aquecida de 0 ºC a 4 ºC ela sofre contração e depois começa a dilatar-se, ou seja, quando a água está em seu estado sólido, ela tem volume maior do que no estado líquido nesse intervalo de temperatura.
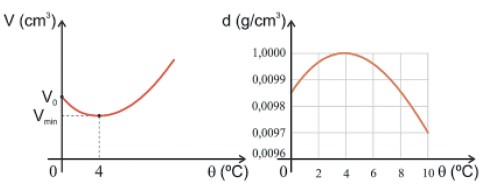
Gráficos da variação do volume e da densidade da água com a temperatura
Se nesse intervalo o volume de água diminui, mantendo-se sua massa constante, a sua densidade será máxima a 4 ºC.
- De 0 a 4ºC: a temperatura aumenta; o volume diminui; a densidade aumenta.
- De 4ºC em diante: a temperatura aumenta; o volume aumenta; a densidade diminui.
O fato de a água possuir esse comportamento se dá por suas moléculas possuírem ligações de hidrogênio que acima de 0ºC, as ligações de hidrogênio começam a romper-se, ocorrendo uma aproximação entre as moléculas. Esse efeito supera a agitação térmica molecular, que causa o afastamento das moléculas e faz com que elas ocupem volume maior de tal forma que ocorre contração em seu volume.
Quando a temperatura supera os 4ºC, o número de ligações de hidrogênio já é bem reduzido. Dessa forma, começa a prevalecer o afastamento molecular, havendo, portanto, aumento em seu volume.
Essa dilatação anômala explica por que a água de um lago congela apenas na superfície. Durante o resfriamento da água até 4 °C, ela fica mais densa e desce para o fundo, fazendo com que água mais quente suba e seja resfriada. Isso ocorre até que toda água esteja a 4 °C. A partir daí, a água em contato com a superfície esfria, mas tem sua densidade reduzida, não desce e acaba se solidificando antes do resto mais ao fundo. Esse gelo formado atua como isolante térmico, dificultando as trocas de calor e preservando o estado líquido no fundo do lado, não matando a vida que ali existe.




