O PONTO NO PLANO
COORDENADAS CARTESIANAS
Sejam os eixos Ox e Oy, perpendiculares em O. Eles determinam um plano (π). Consideremos um ponto qualquer P, P ∈ (π) e tracemos por ele as retas (x’) paralela a Ox e (y’) paralela a Oy. Chamemos P1 e P2, respectivamente, as intersecções de (y’) com o eixo Ox e de (x’) com o eixo Ox.
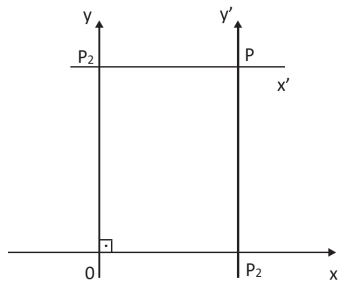
O e P1 determinam o segmento orientado OP1 cuja medida algébrica é a abscissa do ponto P.

O e P2 determinam o segmento orientado OP2 cuja medida algébrica é a ordenada do ponto P.

Os números reais xp e yp constituem um par ordenado que determina a posição do ponto P no plano (π). São as coordenadas do ponto P.
O plano (π) é denominado plano cartesiano e os eixos Ox e Oy que o determinam são os eixos cartesianos, sendo o eixo Ox o eixo das abscissas e Oy o eixo das ordenadas.
xOy indica o sistema de eixos cartesianos ortogonais (ou ortogonais, ou retangulares).
O ponto O é a origem do sistema.
QUADRANTES
Os eixos cartesianos determinam 4 regiões distintas no plano cartesiano, os quadrantes.
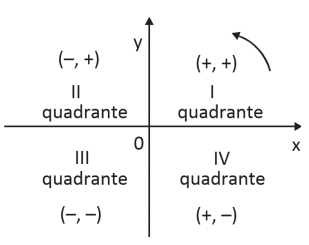
Verificamos facilmente que existe uma correspondência biunívoca entre o conjunto dos pontos P do plano e o conjunto dos pares ordenados (xp , yp).
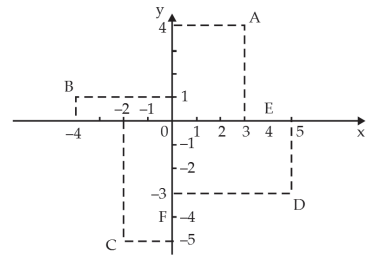
Assim, o ponto A tem sua posição definida no plano cartesiano (π) pelo par ordenado (3, 4) e indicamos por A(3, 4) e lemos ponto A de coordenadas cartesianas 3 e 4.
Da mesma forma os pontos B, C e D.
B(–4, 1), C(–2, –5) e D(5, –3)
Um ponto pertencente ao eixo das abscissas tem ordenada nula.
Se pertencente ao eixo das ordenadas tem abscissa nula, e na origem ambas as coordenadas são nulas, x = y = 0.
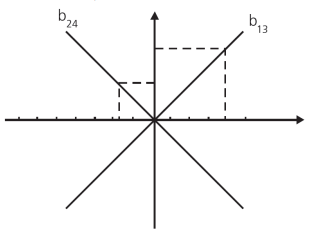
Um ponto pertencente à bissetriz do 1º e 3º quadrantes tem coordenadas iguais e quando pertencente à bissetriz dos quadrantes pares tem coordenadas simétricas.

DISTÂNCIA DE DOIS PONTOS
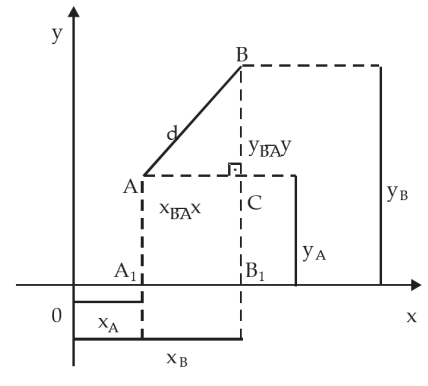
Sejam os pontos A(xA , yA) e B(xB , yB) referidos num sistema de eixos cartesianos ortogonais.
Procuremos a distância d entre dois pontos.

RAZÃO DE SECÇÃO
RAZÃO DE SECÇÃO DE UM SEGMENTO POR UM PONTO
Sejam os pontos A ≠ B ≠ C colineares. Chamamos razão de secção do segmento AB pelo ponto C ao número real r, razão entre as medidas algébricas dos segmentos AC e CB.

Tomemos A(xA , yA) , B(xB , yB) e C(xC , yC).
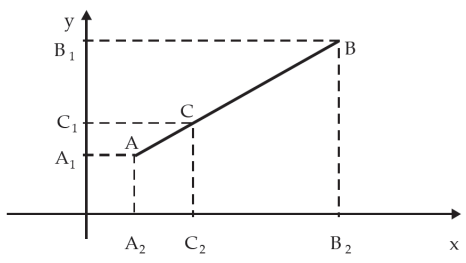
O feixe de paralelas A1A, C1C e B1B determina, sobre as retas AB e OY e o feixe de retas paralelas A2A, C2C e B2B, determina sobre as retas AB e OX segmentos proporcionais, então:

Portanto as coordenadas (x, y) do ponto que divide o segmento compreendido por P1 (x1 , y1) e P2 (x2 , y2) segundo a razão r:

PONTO MÉDIO DO SEGMENTO
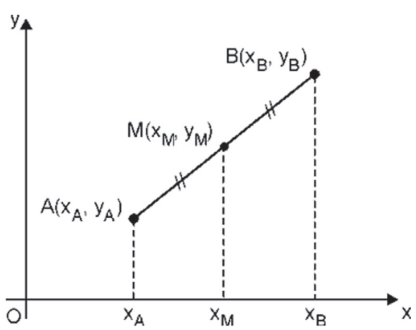
Sendo M(xM , yM) o ponto médio do segmento cujas extremidades são A(xA , yA) e B(xB , yB), tem-se:

BARICENTRO
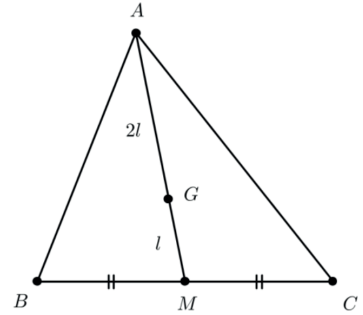
O baricentro de um triângulo é o ponto de concurso de suas medianas. Ele divide cada mediana na razão 2 : 1.

PONTO NO ESPAÇO
Dado um ponto P do espaço, sua posição fica determinada plenamente em relação ao sistema através de suas distâncias PF, PV e PH aos 3 panos coordenados ou pelas projeções destas distâncias sobre os eixos coordenados, respectivamente, AO, OB e OC.
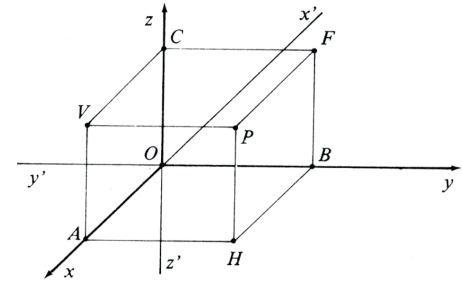
AO = BH = CV = PF = x (abscissa)
OB = AH = CF = PV = y (ordenada)
OC = BF = AV = PH = z (cota)
As fórmulas vistas para o ponto no plano podem ser utilizadas no espaço, acrescentando mais uma coordenada.
DISTÂNCIA ENTRE DOIS PONTOS

BARICENTRO

ÁREA DE UM TRIÂNGULO
Dado um triângulo ABC, de vértices A(x1 , y1), B(x2 , y2), C(x3 , y3), desejamos expressar sua área em função das coordenadas de A, B e C.
Seja r a reta suporte do seguimento BC. A equação de r é dada por:
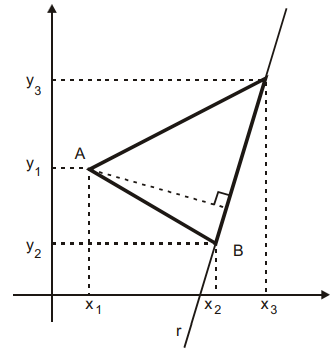



a área do triângulo ABC é igual a (ABC) = 1/2 · d(A,r) ⋅ d(B,C) = desenvolvendo obtemos:


logo a área do triângulo ABC é igual à metade do valor absoluto do “determinante” acima e pode ser calculado da seguinte maneira:
=x1y2 + x2y3 + x3y1 − x2y1 − x3y2 − x1y3
Exemplo:
Calcule a área do triângulo ABC, dados A(1,–1), B(7,5) e C(–2,6).
Resolução:

ÁREA DE POLÍGONOS
Dado um polígono P qualquer, é possível uma divisão de P em triângulos.
Exemplo:
Calcule a área do pentágono ABCDE de vértices: A(3, 0), B(1, 2), C(–2, 2), D(–8, –7) e E(6, –1).
Resolução:

ONDIÇÃO DE ALINHAMENTO DE 3 PONTOS
Sejam os pontos P1(x1 , y1) ≠ P2(x2 , y2) e P3(x3 , y3).
Sabemos que os pontos P1 e P2 determinam a reta (r) da equação

Para P3 pertencer à reta (r) é necessário e suficiente que suas coordenadas satisfaçam sua equação ⇒





