PRINCÍPIO ADITIVO
Se um evento E1 possui α resultados distintos e um segundo evento E2 possui β resultados distintos, sendo E1 e E2 conjuntos disjuntos, então o número de resultados para que ocorra o evento E1 ou o evento E2 é dado pela soma α + β.
Podemos também dizer que há α maneiras de ocorrer o evento E1 ou β maneiras de ocorrer o evento E2. Assim a maneira de ocorrer E1 ou E2 é α + β.
Perceba da noção de conjuntos o uso da conjunção “ou” que nos remete a operação de união.
Exemplo:
Em uma cantina de uma escola há 4 salgados diferentes disponíveis e 3 sabores de sucos distintos. De quantas maneiras uma pessoa pode se servir de um salgado ou um suco?
Perceba que por mais que se tenha vontade de multiplicar 4 · 3 só temos um “espaço” (queremos salgado ou suco). Perceba também que salgado e suco são coisas totalmente disjuntas (distintas), precisamos de um dentre os 7 disponíveis (4 + 3). Isso caracteriza o princípio aditivo.
PRINCÍPIO MULTIPLICATIVO
Se um evento E1 possui αα resultados distintos e um segundo evento E2 independente de E1, possui β resultados distintos, então o número de resultados para o par de eventos (E1, E2) é dado pelo produto α · β.
Podemos também dizer que há α maneiras de ocorrer o evento E1 e β maneiras de ocorrer o evento E2. Assim a maneira de ocorrer E1 e E2 é α · β.
Perceba da noção de conjuntos o uso da conjunção “e” que nos remete a operação de intersecção.
Exemplo:
Uma pessoa tem no guarda-roupas: 3 camisetas, 2 bermudas e dois pares de tênis. De quantas maneiras diferentes essa pessoa pode se vestir?
A pessoa pode usar qualquer uma das três camisetas E dois tipos de bermudas diferentes E dois dos pares de tênis. Como pode usar uma coisa E a outra devemos usar o princípio multiplicativo, daí
3· 2 · 2 = 12
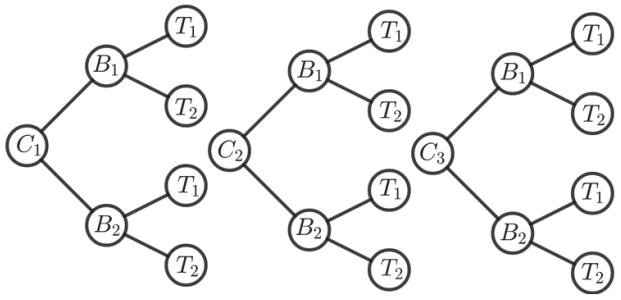
Perceba que uma escolha influencia no caso geral, bermuda azul com camiseta branca é diferente de bermuda vermelha com camiseta branca, por exemplo. Veja que também cabe a montagem da chamada árvore de possibilidades.
FATORIAL
Dado um número natural n ≥ 2, representa-se e define-se o fatorial de n por n! = 1 · 2 · 3 ·…· (n – 1) · n.
Casos particulares: 1 ! = 1 e 0 ! = 1.
Exemplo 1: 2! = 2 · 1! = 2 · 1 · 0! =2 · 1 · 1 = 2
Exemplo 2: 4! = 4 ·3 != 4 · 3 · 2! = 4 · 3 · 2 · 1! = 4 · 3 · 2 · 1 · 0! = 24
Na prática, para calcular o valor de x!, basta multiplicarmos x pelo seu antecessor, e pelo seu antecessor e assim sucessivamente, até número 1, como mostrado abaixo.
x! = x · (x – 1) · (x – 2) · (x – 3) …. 3 · 2 · 1
Atenção: no caso de um fatorial muito grande, é interessante buscar a simplificação em vez de calcular o resultado.
Exemplo: 8!/6! = 8.7.6!/6 = 8 . 7 = 56




