PERMUTAÇÕES SIMPLES
Uma permutação simples de n objetos distintos é uma das sequências ordenadas de n elementos em que os objetos podem ser colocados.
Notacão: Pn (número de permutações simples de elementos distintos).
Propriedade: Pn = n!
Exemplo: de quantas maneiras distintas 5 pessoas podem formar uma fila?
Se pensarmos que cada pessoa é um objeto então também teremos
5 espaços para distribuir esses objetos. Daí usando o princípio multiplicativo teremos que a 1ª posição pode ser ocupada por qualquer um dos 5 objetos. Ocupada a 1ª posição a 2ª posição poderá ser ocupada com qualquer um dos 4 objetos restantes … E assim por diante até que sobra um objeto para o ultimo espaço.
5 · 4 · 3 · 2 · 1
Como essa operação de se multiplicar sequencialmente de um valor n até se chegar ao valor 1 (uma possibilidade), essa operação foi definida como n!. Então a permutação de n objetos é definida como n!. Daí
5 · 4 · 3 · 2 · 1 = P5 = 5! =120
PERMUTAÇÃO COM REPETIÇÃO
Quando precisamos permutar n objetos em n espaços porém, existem objetos repetidos, a permutação se dará de maneira diferente.
Exemplo: Quantos anagramas possui a palavra BANANA?
(Anagrama é a permutação das letras formando-se outra palavra, com sentido ou não).
Como BANANA possui 6 letras (objetos) basta distribuirmos essas letras dentro dos 6 espaços disponíveis. Daí teríamos uma permutação de 6 objetos.
P6 = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Porém vejamos uma das possíveis permutações.
N1 B A1 N2 A2 A3
Perceba que numerando as letras que se repetem podemos ver mais facilmente que se trocarmos de posições as letras N1 com N2 ou as letras A1 com A2 ou com A3, não mudaríamos a palavra, continuaria sendo NBABAA. Então da forma que está teremos contado palavras mais de uma vez, daí precisamos descontar. As 2 letras N podem permutar entre si de 2 ! Maneiras, enquanto as 3 letras A podem permutar entre si de 3! Maneiras. Então para fazer o acerto iremos dividir as 720 maneiras pela quantidade de vezes que as letras repetidas podem permutar entre si.

Daí criamos uma fórmula para permutação quando há objetos repetidos.
“Querendo permutar n objetos em n espaços sendo destes n objetos, a iguais entre si, b iguais entre si, …., até c iguais entre si teremos.

(Tendo objetos que não se repetem, só aparecem uma única vez, não há a necessidade de se dividir por 1!).
PERMUTAÇÃO CIRCULAR
Imagine que devemos distribuir n objetos em volta de uma mesa circular por exemplo (em forma de círculo). Teríamos uma distribuição dessa maneira.
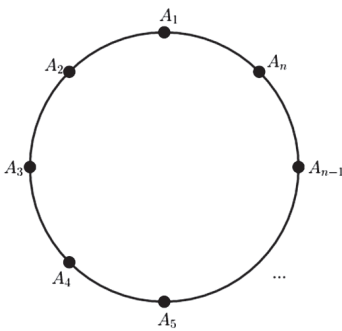
Teríamos Pn = n!, mas repare que podemos “girar” o círculo que a ordem dos objetos não muda.
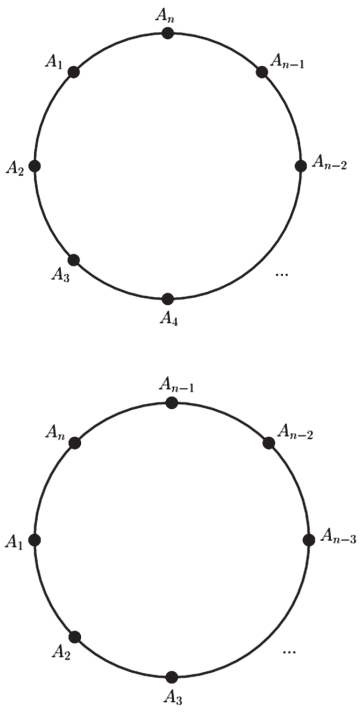
No caso de n objetos podemos girar o círculo n vezes que não alteramos a ordem dos objetos. Então:

Exemplo: De quantos modos distintos podemos distribuir 5 crianças numa roda para se brincar de ciranda?
Como vamos permutar objetos ao longo de um círculo devemos usar uma permutação circular.
Vamos inicialmente permutar as 5 crianças.
P5 = 5 !
Na figura abaixo temos uma das 5 ! Permutações.
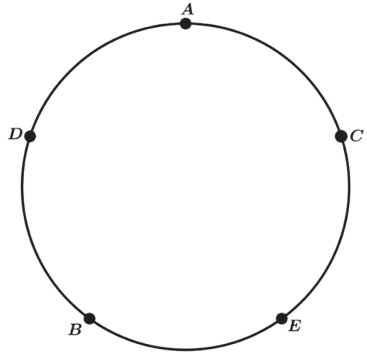
Porém veja que podemos ter 5 “giros” que ainda sim temos a mesma configuração.
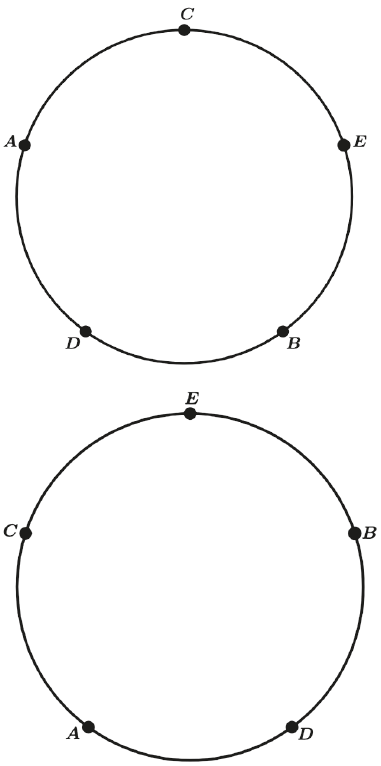
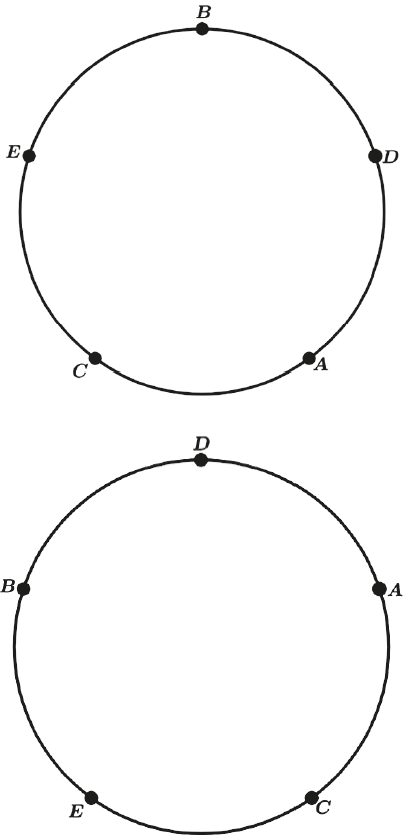
Por isso devemos dividir 5! Por 5, como é a ideia da permutação circular.
5!/5 = 5·4!/5 = 4!
PC5 = P5 – 1 = (5 – 1)! = 4! = 4 . 3 . 2 . 1 = 24




