Contagem: Combinações

OMBINAÇÃO SIMPLES 

Uma combinação simples de n objetos distintos tomados p a p (sendo p ≤ n), é um dos subconjuntos com p elementos em que podem ser colocados p objetos, selecionados entre os n objetos dados.

Notações: C^p_n ou Cn,p (número de combinações de n elementos distintos tomados p a p).

Propriedade: C^p_n = ^n!/_p!(n-p)!

Vamos imaginar que temos os objetos A, B, C, D, E, F e G e que destes queremos escolher 4 objetos. Dentre as vária possibilidades vamos imaginar o seguinte cenário.

ESCOLHIDOS: {A,B,E,F}

NÃO ESCOLHIDOS: {C,D,G}

Podemos começar permutando todos os 7 objetos, ou seja 7!. Mas como queremos 2 grupos, onde não há distinção alguma entre a ordem de seus elementos, tanto que {A,B,E,F}={B,A,F,E}=… tanto para o conjunto de escolhidos como o de não escolhidos devemos dividir 7! Pela quantidade de cada conjunto.

^7!/_4!.3!

Daí temos a noção de combinação simples, de onde sempre que queremos formar um grupo de p objetos dentre n também formamos um outro grupo de (n-p) objetos, assim

C_n,_p = ^n!/_p!.(n-p)!

E dessa ideia podemos perceber que escolher 4 dentre 7 é o mesmo que deixar de escolher 3 dentre 7. Isso se chama combinação complementar.

Escolher p dentre n é o mesmo que escolher (n-p) dentre n. Assim

C_n,p = C_{n,n – p}

Também podemos representar uma combinação simples C_n,p por (ⁿ_p), assim (ⁿ_p) = (ⁿ _{n – p}).

Exemplo: Num restaurante há 8 tipos de saladas, de quantas maneiras distintas uma pessoa pode se servir de 4 saladas diferentes?

Nesse caso é como formarmos um grupo de 4 saladas com as 8 que temos disponíveis. Por exemplo se escolhermos salada de alface (A), rúcula (R), ovos (O) e tomate (T), formamos o grupo de saladas (A, R, O, T). Repare que se trocarmos a ordem das saladas (R, A, T, O), por exemplo, as saladas no prato continuam sendo: alface, rúcula, ovos e tomate. Então ao se formar grupos, onde não há hierarquia ou cargos, a ordem não importa. Essa é a característica da combinação, a ordem não importa. Daí teremos C⁴₈.

Nota: Ao somarmos as combinações de objetos para 0 espaço com a combinação de n objetos para 1 espaço e assim até a combinação de n objetos para n espaços teremos:

C_n,0 +C_n,1 + C_n,2 +… + C_n,n-1 + C_n,n

Isso é o somatório completo de uma linha do triângulo de Pascal, que é igual a 2ⁿ. O somatório das combinações de 0 a n é o mesmo que se fazer o total de subconjuntos. Essa informação pode poupar muitos cálculos numa questão.

C_n,0 + C_n,1 + C_n,2 +…+ C_n,n-1 + C_n,n = 2ⁿ

Exemplo – Uma pastelaria oferece uma promoção: Monte seu pastel com até 5 recheios, carne, queijo, frango, calabresa e pizza. Quantos pastéis diferentes podem ser feitos sabendo-se que um mesmo recheio não pode ser colocado mais de uma vez?

A resposta seria dentre 5 recheios escolhermos somente 1 ou de 5 recheios escolhermos 2 até que de 5 recheios escolhêssemos os 5.

C_5,1 + C_5,2 + C_5,3 + C_5,4 + C_5,5

Onde podemos usar a teoria do somatório do triangulo de pascal para poupar cálculos, mas repare que falta a combinação C_5,0.

A combinação C_n,0 fazendo analogia a teoria de conjuntos essa combinação é equivalente ao conjunto vazio, o que para essa questão não nos interessa pois não queremos pastel vazio. Como C_n,0 é igual a 1, temos:

C_5,1 + C_5,2 + C_5,3 + C_5,4 + C_5,5 = 2⁵ -1 = 32 -1 = 31

COMBINAÇÃO COM REPETIÇÃO

Imagine que você vai a um supermercado e deseja comprar 8 refrigerantes tendo 3 marcas diferentes disponíveis. É fácil perceber que não há possibilidade de levar somente marcas distintas, logo alguma marca terá que se repetir, essa é a ideia da combinação com repetição.

Podemos fazer uma assimilação da combinação com repetição com a quantidade de soluções inteiras e não negativas da equação.

x+y+z=8

Onde x, y e z são as marcas de refrigerante que temos disponíveis e 8 é a quantidade total que queremos levar. Assim veja que se imaginarmos as soluções inteiras e não negativas dessa equação é algo interessante.

Solução {0,3,5} – não compramos nenhum refrigerante da marca 1, 3 refrigerantes da marca 2 e 5 refrigerantes da marca 3.

Solução {2,2,4} – compramos 2 refrigerantes da marca 1, 2 refrigerantes da marca 2 e 4 refrigerantes da marca 3.

Solução {0,8,0} – compramos todos os 8 refrigerantes da marca 2.

Então a quantidade soluções inteiras e não negativas dessa equação nos dá a quantidade de escolhas. Para criar um modo de calcular vamos imaginar cada sinal de + como uma “barra” e a quantidade total que se deseja a quantidade de “bolas” a se distribuir.

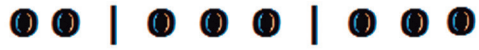
A quantidade de “bolas” que ficarem a esquerda da 1ª barra será a quantidade x.

A quantidade de “bolas” que ficarem entre a 1° e a 2ª barra será a quantidade y.

A quantidade de “bolas” que ficarem a direita da 2ª barra será a quantidade z.

Logo no exemplo teríamos a solução {2,3,3}.

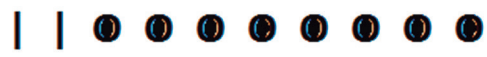
Já essa solução seria {0,0,8},

Então podemos pensar que temos 10 objetos no total (8 bolas e 2 barras), onde 8 são iguais entre si (8 bolas) e 2 são iguais entre si (2 bolas). Logo para se obter uma solução diferente basta permutar a posição dos objetos, assim:

Logo podemos escolher nossos 8 refrigerantes de 45 maneiras diferentes.

Assim quando vamos escolher p objetos dentre n disponíveis mas desses p objetos podemos ter objetos repetidos teremos.

Porém a ideia das bolinhas e barrinhas é sempre mais interessante.