Fique atento às seguintes regrinhas para cálculo de expressões que envolvem uma porção de operações:
I. Se a expressão contiver parênteses, colchetes, chaves, devese iniciar pelas operações indicadas nos sinais mais interiores.
II. As operações de multiplicação e divisão devem ser efetuadas primeiro na ordem que aparecerem (da esquerda para a direita).
III. As adições e subtrações devem ser efetuadas em seguida também na ordem que aparecerem (da esquerda para a direita).
Exemplos:
1) 3+8:4+2·(1·3)=3+2+2·3=3+2+6=11.
2) 7·(3+4:2+2-3(5·3+2)-1)=7·(3+2+2-3(15+2)-1=7.
(7-3·17-1)=7·(7-51-1)=7·-45=-315.
ADIÇÃO
Vamos primeiro entender que estamos trabalhando numa base de numeração decimal, isso quer dizer que temos 10 símbolos (algarismos) {0,1,2,3,4,5,6,7,8,9}. O que isso quer dizer? Que toda vez que uma ordem (posições contadas da direita para esquerda) chega a 10 ou mais devemos ajustar. O melhor exemplo disso é a maneira que vemos a hora. Você não diz que são 13 horas e 72 minutos da tarde porque você sabe que 72 minutos são 60 min +72 min ou seja, 1 h e 12 minutos e assim ajustamos as 13 horas para 14 horas e dizemos o corretor que é: são 14 horas e 12 minutos.
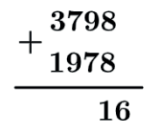
Quando iniciamos o processo de adição começamos a somar do algarismo das unidades para a esquerda. Sempre que essa soma iguala ou ultrapassa 10 unidades em uma mesma ordem nós devemos ver quantos grupos de 10 unidades conseguimos formar e quantas unidades irão formar. Então na verdade fazemos uma divisão por 10.
No nosso exemplo 3798+1978, quando somamos 8+8=16 não podemos escrever 16 em uma ordem, assim temos que dividir 16 por 10 ver o quociente e o resto. Só que dividir por 10 é bem simples e é fácil de ver que o quociente é 1 e o resto 6 . Sendo assim o valor que ocupará a ordem será o 6 e dizemos que sobe 1, a ordem imediatamente superior irá ganhar uma unidade.
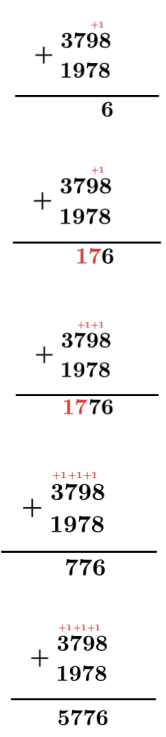
SUBTRAÇÃO
A subtração se dará de maneira semelhante, porém quando tentarmos subtrair um algarismo menor de um maior isso não será possível e assim nós precisaremos fazer o que é chamado de “pedir emprestado ao vizinho”. Só temos que lembrar que esse vizinho da esquerda é uma ordem superior e uma unidade dele vale 10 unidades para quem está à direita. Se 10 minutos emprestar 1 min aos segundos, os segundos não irão estar recebendo, em segundos, 60 segundos? Essa é a ideia.
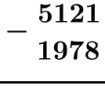
No exemplo de 5121 – 1978 a subtração do algarismo 1 por 8 nāo será possivel fazendo com que o algarismo 2 (ordem imediatamente acima do algarismo 1) empreste uma unidade sua para o 1 e assim o 1 receberá na verdade 10 unidades.
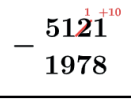
Assim o algarismo 1 ganha 10 unidades e passa a valer 11 e o algarismo 2 perde 1 unidade e passa a valer 1.
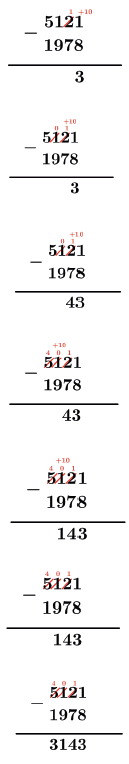
MULTIPLICAÇÃO
Vamos fazer como na adição, sempre que chegarmos a 10 ou mais em uma mesma ordem iremos compensar e um detalhe, cada vez que multiplicamos por um algarismo de uma casa mais a esquerda também movemos o resultado uma casa a esquerda.
Vamos fazer 1346×23:

O que fazemos no produto é o mesmo que 1346×23=1346×(20+3)=1346×20+1346×3.
DIVISÃO
Vamos primeiramente entender o algoritmo da divisão.
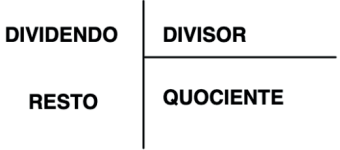
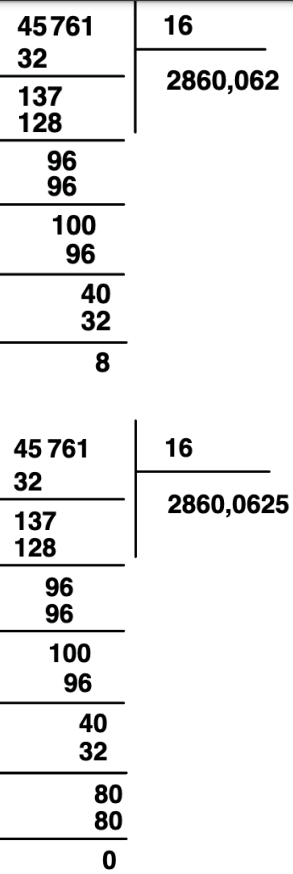
Ao dividirmos um número por outro iremos começar formando um número, com os algarismos da esquerda para direita, maior ou igual ao divisor. Vamos dividir 45761 por 16.
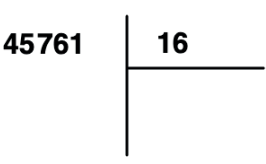
Se pegarmos o 4 sozinho temos 4 < 16. Seguindo pegaremos o 4 junto do 5 formando o 45, 45 > 16.
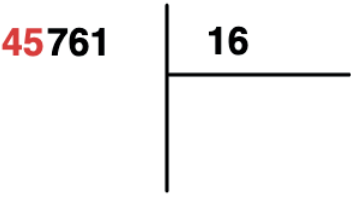
Iremos dividir 45 por 16. Fazemos esta operação por tentativas e vemos por qual valor multiplicamos 16 de modo que que mais próximo ou igual a 45.
16×1=16
16×2=32
16×3=48
Vemos que 16 × 3 ultrapassa então utilizaremos o quociente 2 por enquanto.
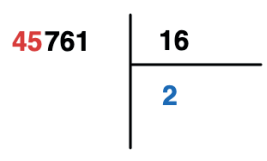
Agora faremos 16 × 2 = 32 e diminuiremos do 45.
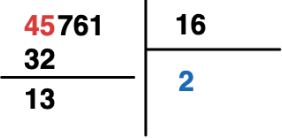
Iremos repetir o processo até que acabem todos os algarismos do dividendo.
16 x 8 = 128
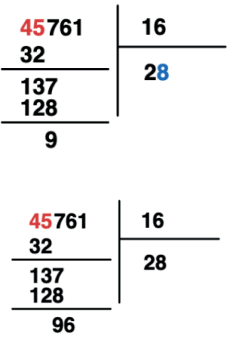
16 x 6 = 96
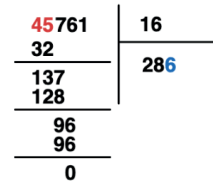
Temos que 1 < 16 e dessa forma adicionamos 0 ao quociente.
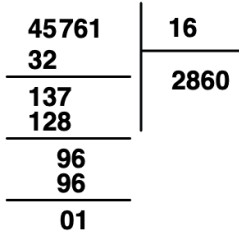
Por fim, não temos mais algarismos para adicionar e dessa forma temos nossa divisão de quociente 2860 e resto 1.
Se quisermos continuar a divisão devemos acrescentar um 0 ao resto e uma vírgula ao quociente
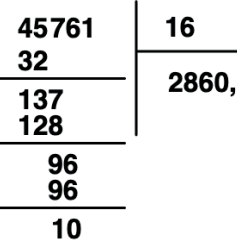
Temos 10 < 16 mesmo após acrescentarmos um 0. Quando temos essa situação o quociente resulta em 0 e assim podemos acrescentar mais um 0 ao resto.
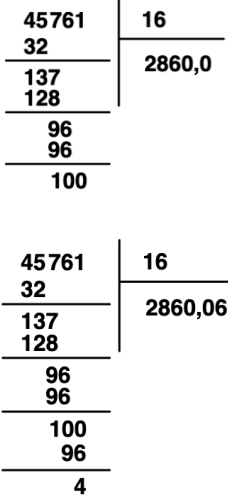
A partir desse momento, todo resto terá o 0 adicionado.
Somente depois de adicionarmos um 0 e ainda assim tivermos o resto menor que o quociente adicionamos um segundo 0 e um 0 no quociente.