Adição e Subtração de Frações
Podem ocorrer dois casos:
I. Os denominadores das frações adicionadas são iguais
a) Para somar frações com denominadores iguais, somamos os numeradores e conservamos o denominador.
b) Para subtrair frações com denominadores iguais, subtraímos os numeradores e conservamos o denominador.
Exemplos:

II. Os denominadores das frações são diferentes
Quando, ao somar ou subtrais frações, os denominadores forem diferentes, devemos reduzir todas as frações ao mesmo denominador. Temos então que determinar o M.M.C. dos denominadores para pode efetuar as operações de adição e/ou de subtração. Se a fração resultante puder ser simplificada, devemos então fazer a simplificação.
Exemplo: efetuar as operações
a) 1/5 + 2/7
Nesse caso os denominadores são diferentes, vamos então determinar o M.M.C. dos denominadores:
M.M.C. (5,7)=35, esse vai ser o denominador comum de todas as frações.
Devemos, em seguida, dividir o M.M.C. encontrado (35), pelo denominador de cada fração e multiplicar o resultado obtido dessa divisão pelo respectivo numerador.

Determinando o M.M.C. dos quatro denominadores: M.M.C. (3,4,8,12)=24, esse vai ser o denominador comum de todas as frações.

Determinando o M.M.C. dos quatro denominadores: M.M.C. (14,7,4,28)=28, esse vai ser o denominador comum de todas as frações.

Como a fração resultante pode ser simplificada (pois M.D.C. $(28,6)=2$, dividimos o numerador e o denominador por 2 , obtendo: 6÷2/28÷2 = 3/14
Essa fração é irredutível e é então o nosso resultado.
Multiplicação de frações
Na multiplicação de fraçőes, devemos multiplicar todos os numeradores das frações envolvidas e devemos multiplicar também todos os denominadores. Para facilitar as contas, podemos fazer simplificações com os números envolvidos, antes de efetuarmos as multiplicações.
Exemplos – Efetuar os produtos:

Na operação acima, antes de efetuarmos as multiplicações, “cortamos” o 2 do numerador com o 2 do denominador.

Na operação acima “cortamos” o 4 do numerador com o 4 do denominador; cortamos o 7 do denominador com o 14 do numerador, sobrando 2 (pois 14/7=2).
Observação: colocamos o 2 em cima do número 14 para mostrar onde foi feita a operação.
Divisão de frações
Na divisão de duas frações, devemos multiplicar a primeira fração pelo inverso da segunda fração.
Exemplos – Efetuar as divisões:

Você deve estar se perguntando:
– Por que invertemos a operação e uma das frações?
Vamos dar essa explicação através de um exemplo simples:

Note que na igualdade: 5/2÷ 3 = 5/2 × 1/3, passamos de uma divisão para a multiplicação do inverso do segundo número e não alteramos o valor da fração original. Fazemos então essa inversão para facilitar as operações.
Potenciação (ou exponenciação de frações)
Na potenciação, quando elevamos um número fracionário a um determinado expoente, devemos elevar o numerador e o denominador a esse expoente.
Exemplos – Efetuar as seguintes potenciações:

RADICIAÇÃO DE FRAÇÕES
Quando aplicamos uma determinada raiz a um número fracionário, aplicamos essa raiz ao numerador e ao denominador.
Exemplos:

Transformações de frações
REDUÇÃO DE NÚMEROS INTEIROS PARA FRAÇÕES IMPRÓPRIAS
Para reduzirmos um número inteiro a uma fração imprópria multiplicamos o número inteiro por uma fração com denominador e numerador iguais à quantidade de partes que vai ser dividida a unidade.
Exemplos
a) Reduzir 7 inteiros a terços.
Nesse caso a quantidade de partes é 3 , então teremos: 7 x 3/3 = 21/3, ou seja, sete inteiros são iguais a vinte e um terços.
b) Reduzir 9 inteiros a quartos.
Nesse caso a quantidade de partes é 4, logo: 9 x 4/4 = 36/4, ou seja, nove inteiros são iguais a trinta e seis quartos
REDUÇÃO DE NÚMERO MISTO PARA FRAÇÃO IMPRÓPRIA
Para reduzirmos um número misto a uma fração imprópria, multiplicamos a parte inteira da fração dada pelo denominador dela e adicionamos esse produto ao numerador da fração e mantermos o mesmo denominador.
Exemplos
Reduzir os números mistos dados a frações impróprias:
a) 3 1/5
Seguindo a regra dada, multiplicamos a parte inteira (3) pelo denominador (5) e somamos com o numerador (1), obtendo-se: (3×5)+1=16. Esse resultado será o numerador da nova fração, cujo denominador (5) será mantido, ou seja: 3 1/5 = (3×5)+1/5 = 15+1/5 = 16/5
b) 7 4/9
Usando o mesmo raciocínio do item (a), teremos: 7 4/9 = (7×9)+4/9 = 63+4/9 = 67/4
CONVERSÃO DE FRAC̣ÃO IMPRÓPRIA PARA NÚMERO MISTO
Dividimos o numerador da fração dada pelo denominador. O quociente dessa divisão será a parte inteira do número misto e o resto será o numerador da fração mantendo-se o mesmo denominador.
Exemplos – Converter as frações abaixo em números mistos:
a) 37/4
Dividimos 37 por 4, o quociente dará 9 e o resto será 1 , observe a divisão:
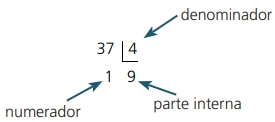
Assim: 37/4 = 9 1/4 ⟺ nove inteiros e um quarto.
b) 25/7
Dividimos 25 pelo denominador 7 , o quociente dará 3 e o resto será 4 , observe a divisão:
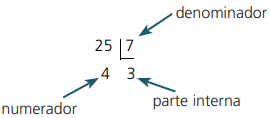
Logo: 25/7 = 3 4/7 ⟺ três inteiros e quatro sétimos.




