NÚMEROS INTEIROS
É o conjunto formado pelos números naturais 1, 2, 3, 4, 5, etc, pelo número 0 e pelos números negativos -1, -2, -3, -4, -5, etc. Costumamos escrever Z=….,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … para denotar esse conjunto. As reticências(….) no início e no final da representação indicam que é possível continuar a escrever tantos inteiros quanto desejarmos, para a esquerda ou para a direita.
Em geral, podemos dizer que:
Para cada número inteiro a existe um número inteiro b tal que a soma dos dois é igual a zero. Esses dois inteiros cuja soma é zero são chamados simétricos.
ADIÇÃO
Adicionar dois números, em termos de campos de ovelhas, consiste em juntar dois campos de ovelhas. Por exemplo, se em um campo, temos 8 animais e em outro temos 9 , no total teremos 8 + 9 = 17 ovelhas.
Observação: Em uma adição, os termos que são adicionados chamam-se PARCELAS e o resultado final chama-se SOMA.
Vejamos as propriedades da adição:
Comutatividade: a ordem das parcelas não altera a soma.
Exemplo: 10+2=2+10=12
Associatividade: se a, b, c são inteiros, então a+(b+c)=(a+b)+c
Exemplo: 9+(3+5)=(9+3)+5=17
Elemento neutro: o zero (0) é o elemento neutro da adição, ou seja, zero adicionado a qualquer coisa não influi no resultado. Matematicamente, a+0=0+a=a.
Exemplo: 7+0=0+7=7
Simétrico: para todo inteiro a, a+(-a)=0. (-a) é dito o simétrico de a.
Exemplo: 3+(-3)=0
SUBTRAÇÃO
A subtração é a operação inversa da adição. Pensando em campos de ovelhas, imagine que em uma noite, temos 12 ovelhas no campo. Durante a madrugada, uma raposa come 4 das 12 ovelhas. Quantas restarão? A resposta é $12-4=8$. Matematicamente, definimos a-b=a+(-b).
Observação 1: na subtração a-b=c, temos que a é dito MINUENDO, b é o SUBTRAENDO e c é o RESTO.
Observação 2: Guarde a seguinte relação fundamental – “MINUENDO = SUBTRAENDO + RESTO”
MULTIPLICAÇÃO
A multiplicação é, essencialmente, uma soma de vários termos iguais. Em termos de campos de ovelhas, multiplicar dois números é a mesma coisa que juntar vários campos de ovelhas com a mesma quantidade de ovelhas em cada um. Por exemplo, se temos três campos com quatro ovelhas em cada um, no total teremos 4+4+4=4·3=12 ovelhas no total. Matematicamente, se a e b são naturais, temos que:

Vejamos as propriedades da multiplicação:
Comutatividade: a ordem dos fatores não altera o produto
Exemplo: 8·1=2·8=16
Se a, b são naturais, então a·b=b·a
Associatividade: se a, b, c são naturais, então a·(bc)=(ab)·c
Exemplo: 2·(3·6)=(2·3)·6=36
Elemento Neutro: a unidade é o elemento neutro da multiplicação.
Exemplo: 5·1=1·5=5
Se a é natural, então a·1=1·a=a
Distributividade: se a, b, c são naturais, então a·(b+c)=a·b+a·c
Lei do Corte: se a, b, c são naturais, com a diferente de 0 , tais que a·b=a·c, então b=c.
Observação: em axb/c, temos que a é o MULTIPLICANDO, b é o MULTIPLICADOR e c é o PRODUTO.
Para a e b inteiros, multiplicamos inicialmente os números retirando o sinal. O resultado será o produto obtido com um sinal que será determinado pela seguinte regrinha de sinais (que pode ser demonstrada pela propriedade distributiva da multiplicação):
O produto de dois inteiros de sinais contrários é um inteiro negativo e o produto de dois inteiros de mesmo sinal é positivo.
Exemplos:
2·(-3)=-6
(-3)·(-5)=15
DIVISÃO
A divisão é basicamente a operação inversa da multiplicação. O nosso resultado fundamental é o seguinte, seguindo o exemplo.
Dados dois inteiros D e d, existem inteiros q, r, unicamente determinados, tais que D=d·q+r e 0≤r<|d|.
(Guarde bem essa relação! Ela será MUITO MUITO útil! Nunca se esqueça da condição 0≤r<|d| !!!!).
Podemos montar o seguinte esquema:
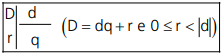
Nessa operação, D é chamado de dividendo, d divisor, q quociente er resto.
|x| representa o chamado valor absoluto (ou módulo de x). É uma definição super simples:
quando x é maior ou igual a 0,|x|=x. Quando x é negativo, |x|=-x.
Exemplos:
1) Ache o quociente e o resto de 42 na divisão por 5. Temos que 42=5·8+2. Como 0≤2<|5|=5, temos que 2 é o resto de 42 na divisão por 5 e que 8 é o quociente.
2) Ache o quociente de -31 na divisão por 4. Temos que -31 = 4 · (-8) + 1. Como 0 ≤ 1 < |4| = 4, temos que 1 é o resto de -31 na divisão por 4 e que -8 é o quociente.
Observação: se o resto da divisão é igual a 0, a divisão é dita EXATA.
Propriedades da divisão
- Numa divisão exata, multiplicando-se o dividendo por um número kk∈ℕ*, o quociente ficará multiplicado por esse número.
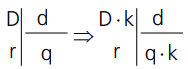
- Numa divisão exata, multiplicando-se o divisor por um número kk∈ℕ*, o quociente ficará dividido por esse número.
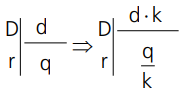
- Numa divisão exata, dividindo-se o divisor por um número k(k∈ℕ*, o quociente ficará multiplicado por esse número.
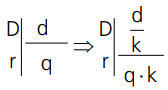
- Numa divisão exata, o quociente não se altera, quando multiplicamos o dividendo e o divisor por um mesmo número kk∈ℕ*, mas o resto fica multiplicado por esse número
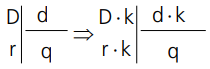
O maior resto R em uma divisão inexata é igual ao divisor menos 1.
Numa divisão inexata, o maior número N que devemos subtrair do dividendo sem alterar o quociente é igual ao próprio resto.
Ache o quociente de -43 na divisão por -5 .
Temos que -43=(-5) · 9 + 2. Como 0 ≤ 2 < |-5| = 5, temos que 2 é o resto de -43 na divisão por -5 e que 9 é o quociente.




