Como exemplo, tem-se que a soma de dois números naturais é sempre um número natural, ou seja, diz-se que o conjunto dos naturais é fechado na operação adição.
CONJUNTOS DOS NATURAIS
ℕ={0,1,2,3,4,5,6,…}
O conjunto dos naturais é fechado nas operações de adição e multiplicação, ou seja, se a,b∈ℕ então a+b∈ℕ e a·b∈ℕ.
O conjunto dos naturais não é fechado nas operações de subtração e divisão.
Exemplo:
2 e 3∈ℕ, porém 2-3=-1∉ℕ e 2/3=0,6666…∉ℕ. .
O conjunto dos naturais positivos, denotado por ℕ*, é o conjunto dos naturais excluindo o zero, ou seja, ℕ*-{0}.
ℕ⋆={1,2,3,4,5,6…}
Propriedades
Sejam a,b,c ∈ℕ, tem-se que:
Tricotomia: é sempre verdade que a=b ou a<b ou a>b.
Transitividade:
Se a=b e b=c, então a=c.
Se a>b e b<c, então a<c.
Associatividade:
Adição: (a+b)+c=a+(b + c).
Comutatividade:
Adição: a+b=b+a.
Multiplicação: a·b=b·a
Elemento neutro:
Adição: a+0=0+a=a.
Multiplicação: a·1=1·a=a.
Distributividade: a·(b+ c)=ab + ac
Lei do corte:
Adição: se a+b=a+c, então b=c.
Multiplicação: se a·b=a·c e a ≠ 0, então b = c.
CONJUNTO DOS INTEIROS
ℤ={…,-3,-2,-1,0,1,2,3,…}
O conjunto dos números inteiros é fechado nas operações de adição, subtração e multiplicação, ou seja, se a,b∈ℕ então a+b∈ℕ, a-b∈ℕ e a·b∈ℕ.
O conjunto dos números inteiros não é fechado na operação divisão.
Exemplo:
é-2 e 3∈ℤ, porém-2/3=-0,6666…∉ℤ
Subconjuntos importantes do conjunto dos números inteiros:
Inteiros não-nulos: ℤ*={…,-3,-2,-1,1,2,3,…}
Inteiros não-negativos: ℤ+=ℕ={0,1,2,3,…}
Inteiros não-positivos: ℤ-={…,-3,-2,-1,0}
Inteiros positivos: ℤ+*={1,2,3,…}
Inteiros negativos: ℤ-*={…,-3,-2,-1}
Propriedades
Simétrico ou Oposto de um número: se a∈ℤ, então -a∈ℤ tal que a+(-a)=(-a)+a=0.
Atenção: Valor Absoluto ou Módulo de um Número Inteiro.

Exemplo:
|2|=2
|-2|=-(-2)=2
CONJUNTOS DOS NÚMEROS RACIONAIS
Número racional é o número que pode ser colocado na forma p/q, em que p e q são números inteiros, q é diferente de zero e mdc (p, q)=1, ou seja, ℚ={p/q ∣ p ∈ ℤ, q ∈ ℤ* e mdc (p, q)=1.
Os racionais podem ser representados por:

Os números inteiros são também números racionais, pois podem ser considerados frações de denominador 1.
O conjunto dos números racionais é fechado nas quatro operações, ou seja, se a, b ∈ ℚ então a + b ∈ ℚ, a – b ∈ ℚ, a · b ∈ ℚ e a/b ∈ ℚ.
Exemplo:

Operações com números racionais:

Fração geratriz
Operação para obtenção da fração geratriz de uma dízima periódica:
- toma-se o número até o final do primeiro período (ignorar a vírgula);
- diminui do número até o início do primeiro período;
- divide por tantos noves de acordo com a quantidade de algarismo do período;
- acrescenta-se zero ao denominador de acordo com a quantidade de algarismos do ante período.
Exemplo:

CONJUNTOS DOS NÚMEROS REAIS
O conjunto dos números reais ℝ é resultado da união do conjuntos dos números racionais (ℚ) com o conjunto dos números irracionais (I), ou seja, ℝ=ℚ∪ 𝕀. O conjunto dos números irracionais é formado por números infinitos, decimais e não-periódicos, ou seja, números que não podem ser representados na forma de fração.
Exemplo:
Raízes inexatas: √2, √3, ³√4 e ⁴√5
Dízimas não periódicas: 0,123456…,π=3,1416, e=2,7182
O conjunto dos números reais é fechado nas quatro operações, ou seja, se a,b ∈ ℝ então a + b ∈ ℝ, a-b ∈ ℝ, a · b ∈ ℝ e a/b ∈ ℝ.
ℝ=ℚ∪𝕀 ou ℚ=ℝ-𝕀 ou 𝕀=ℝ-ℚ.
ℕ⊂ℤ⊂ℚ⊂ℝ, ou seja,
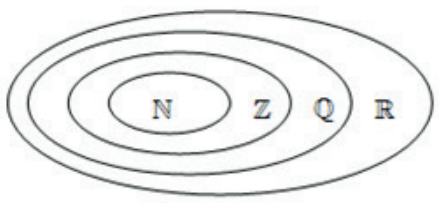
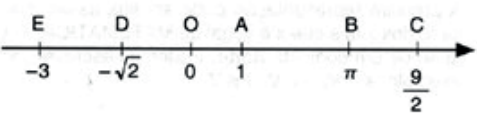
O conjunto ℝ pode ser representado por uma reta orientada que recebe o nome de reta real.
O conjunto dos números irracionais não é fechado nas quatro operações, pois, a,b ∈ 𝕀 então, a + b ∈ l ou a + b ∈ ℚ, a – b ∈ I ou a – b ∈ ℚ, a · b ∈ l ou a · b ∈ ℚ e a/b ∈ I ou a/b ∈ ℚ.
Exemplo:





