Cone

CONE CIRCULAR

Considere um círculo R contido num plano α, e B um ponto que não está em α. O conjunto de todos os segmentos de reta que unem os pontos de R ao ponto B formam um cone circular.

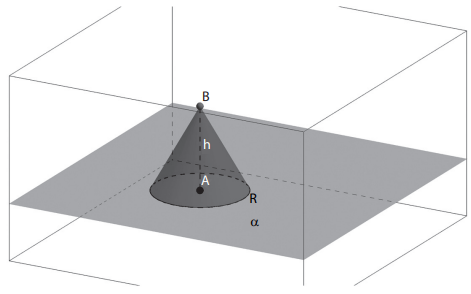
A reta que passa pelos pontos A, centro da base, e o ponto B, é o eixo do cone.

No caso o segmento AB é perpendicular à base, o cone é circular reto, caso contrário será oblíquo.

DEFINIÇÕES

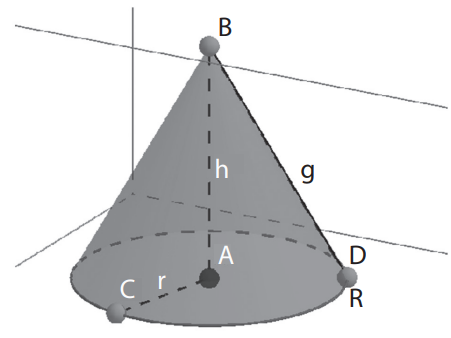
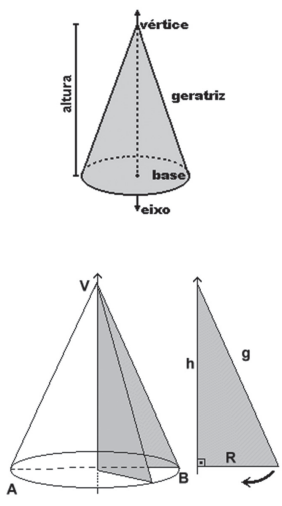
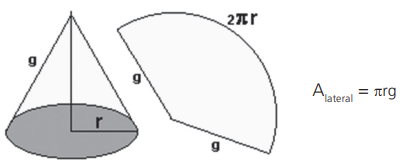
No cone circular reto o segmento que une os pontos A e B é chamado de altura e o segmento que une os pontos B e C é chamado de geratriz, B é o vértice do cone e o círculo R é a base do cone, a distância de A até C é o raio da base.

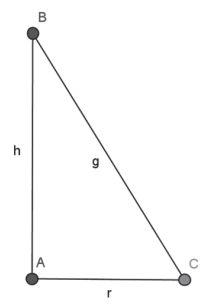
No cone circular reto vale a seguinte relação g² = r² + h².

CONE OBLÍQUO

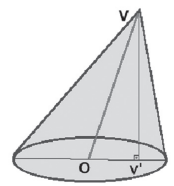
CONE CIRCULAR RETO OU CONE DE REVOLUÇÃO

O cone circular reto é criado pela rotação de um triângulo retângulo em torno de um dos seus catetos. Este é o motivo pelo qual a superfície de um cone recebe o nome de superfície de revolução.

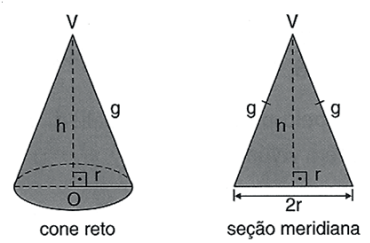
SEÇÃO MERIDIANA E CONE EQUILÁTERO

Seção meridiana de um cone é a intersecção dele com um plano que contém o eixo. A seção meridiana de um cone reto é um triângulo equilátero.

Cone equilátero é um cone cuja seção meridiana é um triângulo equilátero.

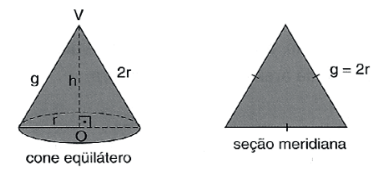
Assim

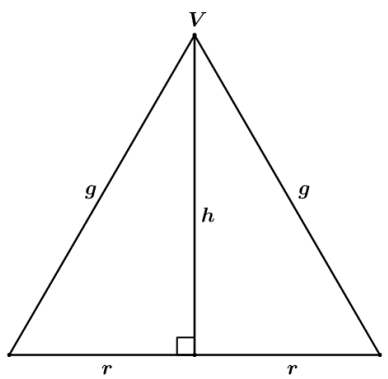
Dessa forma, sendo nossa seção meridiana um triângulo equilátero, teremos que:

Assim teremos também:

ÁREA LATERAL (cone reto):

SÓLIDOS DE REVOLUÇÃO

Sólidos de revolução são sólidos circulares formados pela rotação de 360° de uma superfície plana (polígono qualquer) de área S em volta de um eixo de rotação previamente definido.

Vamos ilustrar aqui diferentes sólidos de revolução.

Para efeito do nosso estudo vale ressaltar que para polígonos que possuem simetria em relação a um eixo, como triângulos equiláteros, quadrados, retângulos, será indiferente rotacioná-los integralmente ou apenas uma das “metades” em relação ao eixo de simetria.

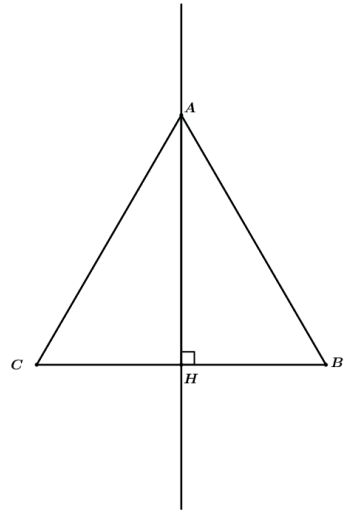
Por exemplo, rotacionar todo o triângulo isósceles ABC abaixo em relação a altura AH é o mesmo que rotacionar o triângulo ABH em relação ao lado AH.

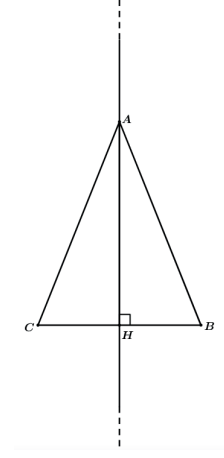
Os triângulos ABH e ACH são congruentes, daí rotacionar ABH ou ABH ou até mesmo ACH em torno da reta suporte de AH resultará no mesmo sólido de revolução que será um cone reto.

CILINDRO RETO

O cilindro reto é resultado da rotação de um retângulo em torno de algum de seus lados.

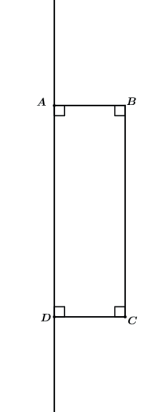
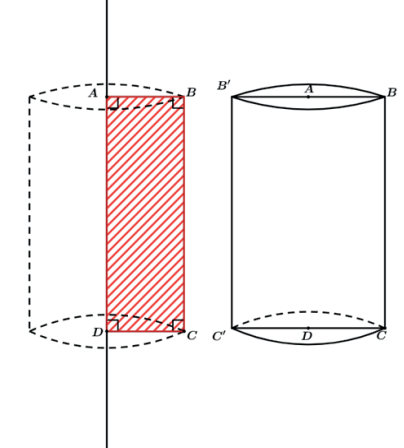
Ao rotacionarmos o retângulo ABCD acima em torno de um de seus lados, por exemplo o lado AD, teremos que a área do retângulo ABCD irá “varrer” uma região no espaço.

Assim o resultado será o cilindro reto de raio das bases CD (segmento que ficou na horizontal) e altura AD (segmento que ficou na vertical).

CILINDRO EQUILÁTERO

O cilindro equilátero é o resultado da rotação de um quadrado em relação ao seu eixo de simetria (reta que liga os pontos médios dos lados).

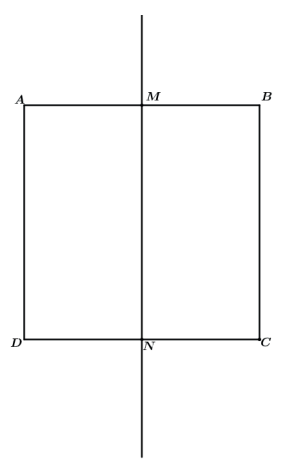
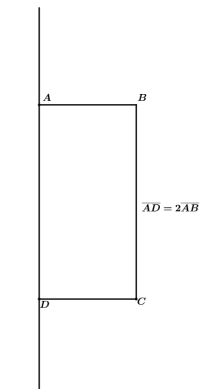
Ou do retângulo que possua uma dimensão igual ao dobro da outra, sendo rotacionado sobre a reta suporte do maior dos lados.

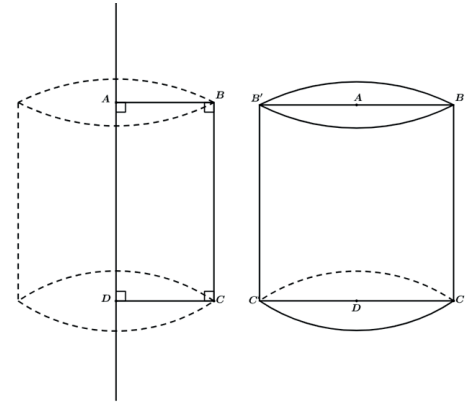
CONE RETO

O cone reto é resultado da rotação de um triângulo retângulo em torno de um de seus catetos.

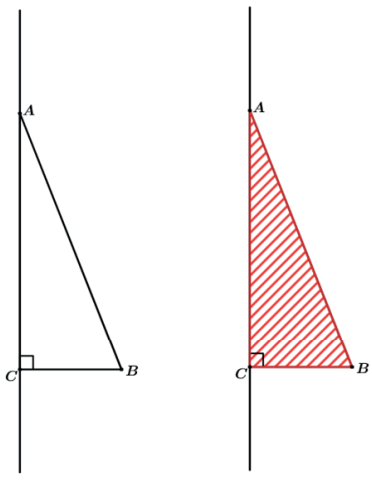
Assim o resultado será o cone reto de raio da base BC (segmento que ficou na horizontal) e altura AC (segmento que ficou na vertical).

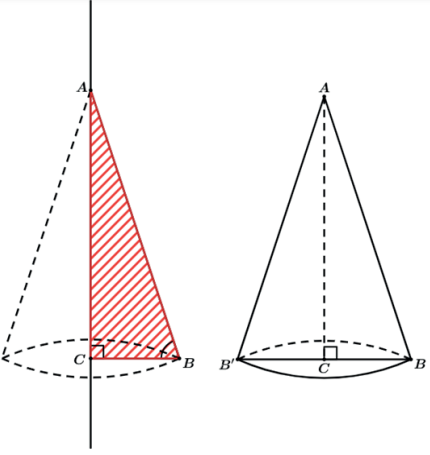
Um detalhe interessante é que o lado AB é o responsável por formar a geratriz do cone.

CONE EQUILÁTERO

O cone equilátero é o resultado da rotação de um triângulo equilátero em relação a sua altura.

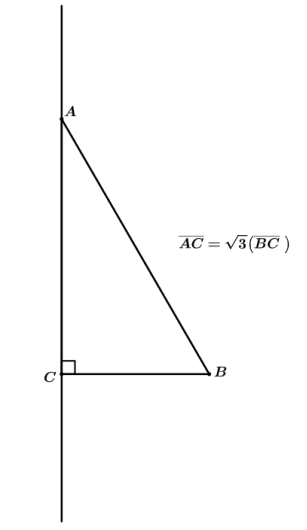
Ou do triângulo retângulo que possua um cateto medindo √3 vezes a medida do outro cateto, sendo rotacionado sobre o maior dos catetos.

DOIS CONES RETOS

Até aqui vimos apenas sólidos de rotação resultantes de rotações de polígonos em relação a um eixo de simetria perpendicular a um de seus lados. Vamos pensar por exemplo se fizermos a rotação do triângulo ABC abaixo em relação a reta suporte do lado BC, o que vamos obter?

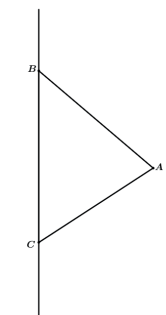
Vamos traçar a altura relativa ao lado BC e olhar novamente.

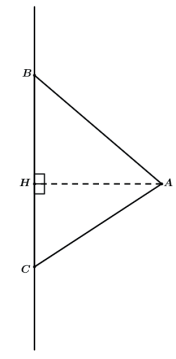
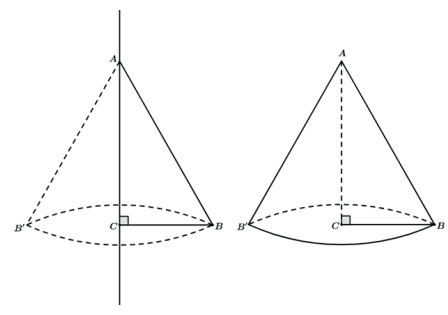
Cada um dos triângulos, ABH e ACH, será responsável por “varrer” uma região que delimitará um cone reto cada.

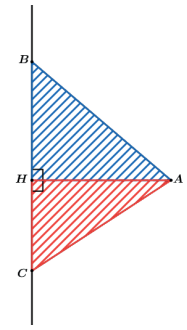
O cone gerado pelo triângulo ABH (hachurado de azul) possuirá raio da base AH e altura BH enquanto o cone gerado pelo triângulo ACH (hachurado de vermelho) possuirá raio da base AH e altura CH. Assim teremos 2 cones formados.

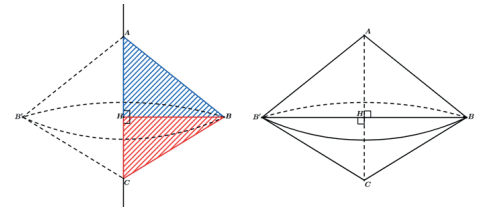
Exemplo:

Calcular o volume do sólido obtido pela rotação de 360° do triângulo retângulo de lados medindo 3 cm, 4 cm e 5 cm em torno da reta suporte da hipotenusa.

Primeiramente deveremos encontrar a medida da altura relativa a hipotenusa BH.

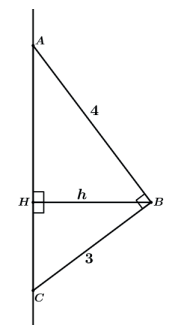
Para isso utilizaremos as relações métricas no triângulo retângulo.

Assim ao rotacionarmos o triângulo ABC teremos como resultado os 2 cones retos abaixo.

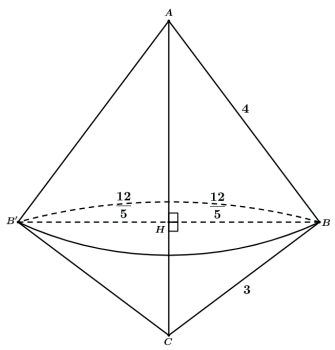
Perceba que não precisamos encontrar as medidas de AH e CH, mesmo sendo possível também utilizando relações métricas no triângulo retângulo, pois para o cálculo volume só será necessário a medida de todo o lado AC.

Vamos ver agora alguns exemplos de sólidos de revolução “vazados”, aqueles que temos de imaginar um sólido maior sendo diminuído de um ou mais sólidos menores.

Exemplo:

Calcule o volume do sólido de revolução gerado pela rotação de 360° do triângulo ABC em relação ao lado AB sabendo que AB = 4 cm, BC = 6 cm e AB^{^}C = 150^∘.

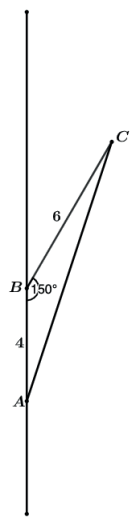
Primeiramente teremos que encontrar a altura relativa ao lado AB, ou a projeção do vértice C sobre o eixo de rotação.

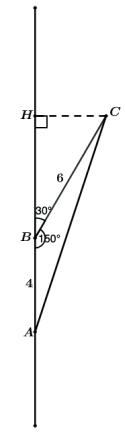
Aplicando razões trigonométricas no triângulo BCH podemos encontrar o valor de CH.

Assim quando fizermos a rotação do triângulo ABC veremos que o sólido gerado é resultado de um cone reto “maior”, gerado pelo triângulo ACH diminuído de um cone reto “menor” gerado pela rotação do triângulo BCH. Onde dizemos que o volume gerado pela rotação de BCH é um volume não útil.

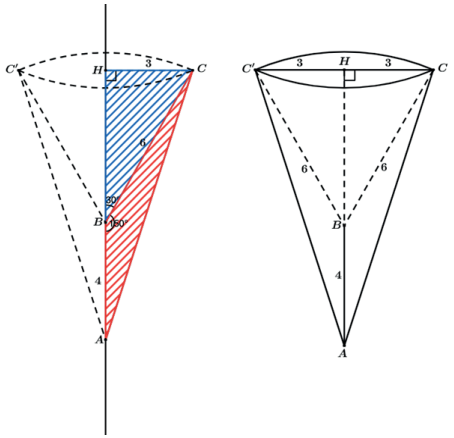
Assim o volume procurado é o volume do cone ACC’ subtraído do cone BCC’.

Como AH − BH = AB, teremos

Geralmente teremos sólidos vazados quando a rotação se der em torno de uma reta paralela a um dos lados do polígono. Vejamos alguns exemplos.

Exemplo

Sólido de revolução gerado pela rotação de um retângulo ABCD, em torno de uma reta r, paralela a AB e distando d de AB.

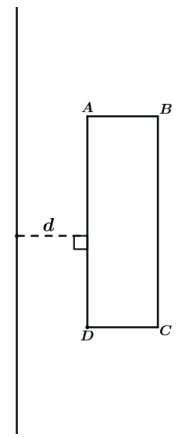
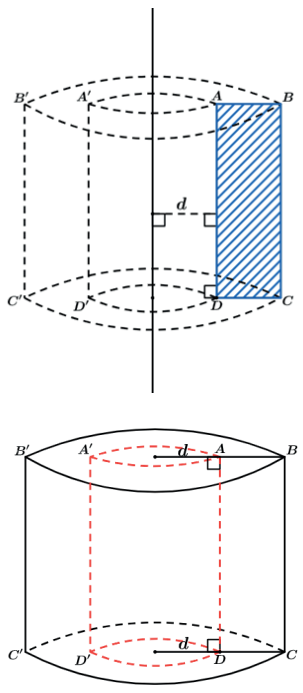
O sólido gerado é um cilindro “furado”, ou um anel cilíndrico. O volume final será o volume do cilindro maior BCC’B’ subtraído do cilindro menor ADD’A’.