EQUAÇÃO DA POSIÇÃO VERTICAL DOS ELEMENTOS DE CORDA EM FUNÇÃO DE X E DE T
A figura abaixo mostra uma possível configuração de uma onda produzida em uma corda em três instantes diferentes, t1, t2, t3.
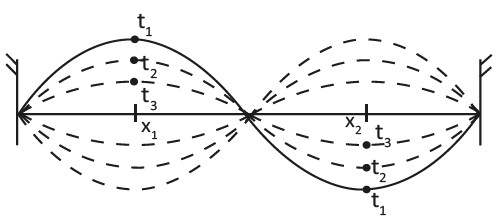
Perceba que no instante t1, o elemento da corda 1 está na crista da onda e na direção vertical que passa por x1. Nesse mesmo instante, em x2, o elemento da corda 2 está no vale. Note também que, conforme o tempo vai passando, o elemento 1 está descendo, enquanto 2 está subindo.
Isso significa que a altura dos elementos de corda dependem de x e de t. Como os elementos da corda estão em M.H.S., para um determinado x, temos:

que corresponde à equação da posição y em função do tempo em um movimento harmônico simples.
Fazendo ω = 2π/T e relacionando esse tempo T (período) com o tempo para o deslocamento de uma onda completa λ, teremos a equação da posição y de um elemento de corda para um dado x em um instante t qualquer:

ou ainda:

Em que k = 2π/λ é chamado de número de onda. Assim como 1/T significa o número de oscilações por segundo (frequência) e ω = 2π/T, podemos entender que 1/λ exprime o número de comprimentos de onda por unidade de comprimento. Portanto, a relação entre k e λ é análoga à relação entre ω e T.
Observação: Se a propagação for para a direita, usaremos o sinal negativo, e se for para a esquerda, positivo. Portanto:
y(x, t) = Acos[kx – ωt + ϕ] → direita
y(x, t) = Acos[kx + ωt + ϕ] → esquerda
Exercício Resolvido 1: Uma onda se propaga com velocidade de 1 m/s para a direita em uma corda conforme figura a seguir:
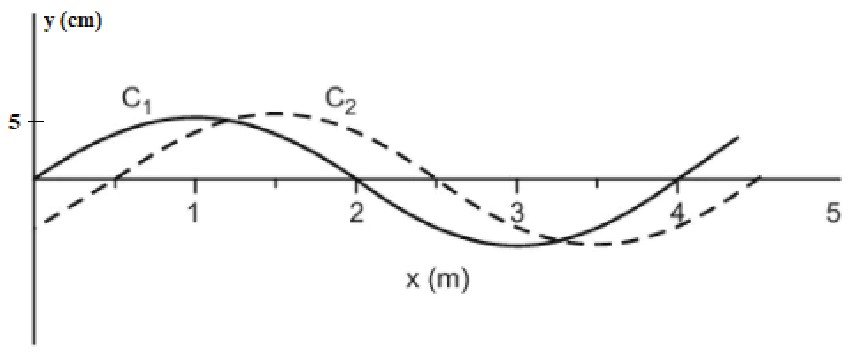
Qual é a equação que relaciona a posição vertical dos elementos dessa corda em função de x e de t?
Resolução:
Para determinarmos a equação da onda, temos que achar as grandezas A, k, ω e ϕ.
No tempo t = 0, o elemento que está em x = 0 está na altura y = 0. Portanto:
y(x, t) = Acos[kx – ωt + ϕ]y(0,0) = Acos[k ⋅ 0 – ω ⋅ 0 + ϕ] = 0 ∴ ϕ = ± π/2rad
Como saber se o ângulo inicial é + π/2 rad ou – π/2rad?
Uma dica: veja se esse ponto irá subir ou se irá descer (é o que acontece nesse exemplo. Basta ver que, em x = 0, a linha pontilhada está abaixo da linha contínua). A velocidade desse elemento de corda é calculada derivando a equação da posição:

Tomando t = 0 e x = 0, obteremos:
vy(0, 0) = –ωAsin[k ⋅ 0 – ω ⋅ 0 + ϕ] = – ωAsin[ϕ]
Como a velocidade é negativa nesse ponto,
ϕ = π/2rad → vy(0,0) = – ωAsin[π/2] = – ωA
Portanto,

A figura nos informa que λ = 4 m e o enunciado nos informou a velocidade da onda. A frequência de oscilação dessa corda é, então:

Já o número de onda k pode ser facilmente obtido, usando-se a relação abaixo:

E a amplitude A vale 5 cm. Como a questão não pede para colocar a medida de y no S.I., podemos escrever a equação como:

Ou ainda, simplificando:

EQUAÇÃO DE TAYLOR
Sabemos que, como a onda em uma corda é uma onda transversal, uma força vertical deve ser aplicada sobre a corda. É uma força tensora (tração T→). A figura a seguir mostra um pulso da corda sob a aplicação dessa força:
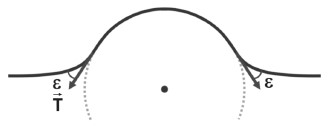
Suponha que o pulso formado tenha um formato de um pequeno arco de círculo de raio r e com um pequeno ângulo de abertura 2ε, conforme figura acima. A resultante das forças que atua no elemento dm será vertical para baixo, apontando para o ponto O, que é a resultante centrípeta. Logo:

Temos também que dl = 2rε. Substituindo na equação acima, teremos:

Fazendo sen ε ≈ εe dm/dl = m/l = μ, já que a corda é homogênea, ou seja, a densidade de um pequena parte dela é igual à densidade da corda toda, teremos que:

A equação acima é a equação de Taylor, que nos mostra a relação entre a força T aplicada na corda, sua densidade linear µ (massa/comprimento) e a velocidade de propagação da onda na corda. Podemos perceber que uma mesma força aplicada em cordas de densidades diferentes produz ondas com velocidades diferentes e, consequentemente, frequências diferentes. É o que acontece em um violão (as cordas do violão têm densidades diferentes. As mais densas produzem sons mais graves). Veremos essa situação no módulo de Acústica.
Relacionando a frequência da onda produzida em uma corda com a força T nela aplicada, obteremos:

Exercício Resolvido 2: (UFJF-PISM 3 2017 ADAPTADA) Consideremos uma corda fixa nas suas extremidades e sujeita a certa tensão. Se excitarmos um ponto desta corda por meio de um vibrador de frequência qualquer ou pela ação de uma excitação externa, toda a extensão da corda entra em vibração. É o que acontece, por exemplo, com as cordas de um violão. Existem certas frequências de excitação para as quais a amplitude de vibração é máxima. Estas frequências próprias da corda são chamadas “modos normais de vibração”. Além disto, formam-se ondas estacionárias, exibindo um padrão semelhante aquele mostrado na figura 1a.
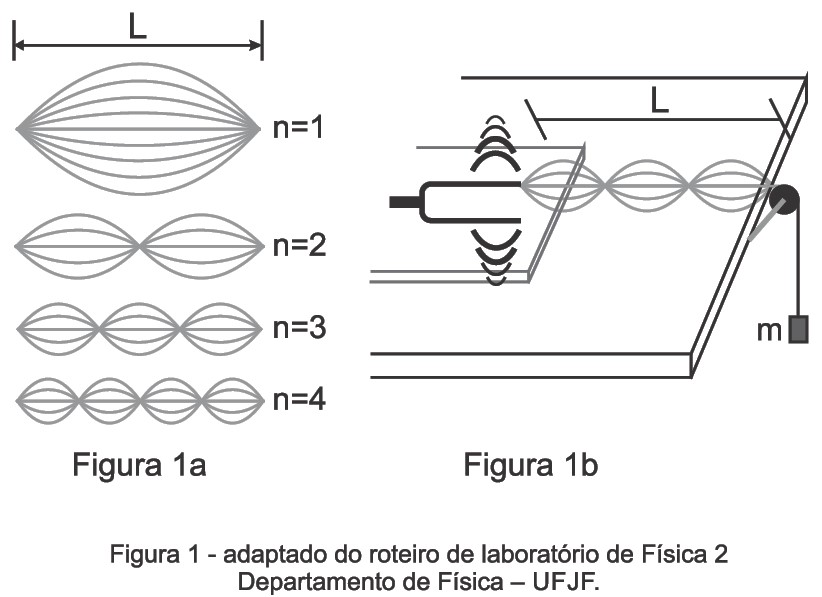
Com base nestas informações, um estudante usou o laboratório didático de sua escola e montou o seguinte experimento: uma corda tem uma de suas extremidades presa a um diapasão elétrico que oscila com frequência constante e a outra extremidade passa por uma polia na extremidade de uma mesa e é presa a uma massa m pendurada do lado de fora, conforme ilustrado na figura 1b.
No experimento, foi usado um diapasão elétrico de frequência constante f = 150 Hz. Ele fixou a corda para um comprimento L = 80 cm e massa 80 g. Nesta configuração, obteve o padrão de oscilação da corda formando 3 ventres, conforme a figura 1b. Qual é a massa do bloco m que está tensionando a corda?
Resolução:
A configuração apresentada de 3 ventres é conhecida como 3º harmônico. A primeira configuração, por exemplo, é a mais simples possível, chamada de harmônico fundamental. Como 3 ventres equivalem a 1,5λ, temos que:

O diapasão faz com que a corda vibre na mesma frequência que ele; estão em ressonância (fenômeno que será explorado no módulo 18). A velocidade dessa onda é:

A densidade linear da corda vale μ = m/L = 0,08/0,8 = 0,1 kg / m. Assim, a tensão à que essa corda está submetida vale:

e, como a tração do fio tem o mesmo módulo que a força peso do bloco, temos que sua massa vale incríveis 64 kg.




