Consideremos uma partícula lançada de um ponto O. A partícula será lançada, com uma velocidade inicial v0→, sob um ângulo θ com a horizontal que será chamado de ângulo de lançamento ou ângulo de tiro.
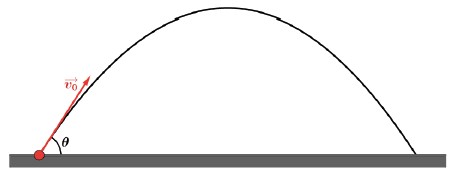
Vamos considerar dois eixos orientados, x e y, com origem no ponto O. Vamos decompor a velocidade v0→ em dois vetores perpendiculares, vx→ e vy→.
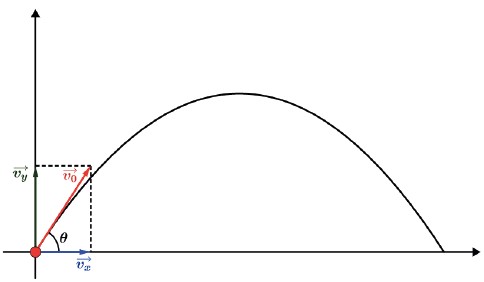
A partícula irá percorrer uma trajetória onde destacaremos a altura máxima (H) e o alcance (A), distância medida horizontalmente a partir do ponto O de lançamento.
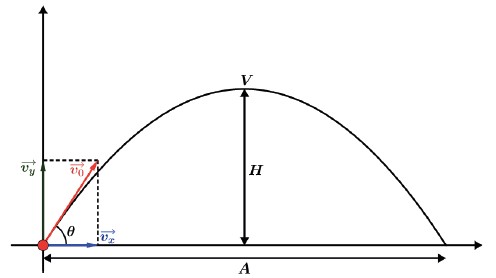
A análise de todo o movimento da partícula, durante todo o lançamento, será dada pelo estudo dos movimentos na vertical e horizontal de maneira isolada. Na vertical iremos considerar como um lançamento vertical, onde a velocidade v0 → tem seu módulo diminuído, pela ação contrária da gravidade no movimento, até que chega na altura máxima do movimento, ponto este que a velocidade vertical é nula. A partir desse momento há a inversão do sentido do movimento e a velocidade vertical vy → começa a ter seu módulo aumentado, mas agora no mesmo sentido da gravidade. Na horizontal teremos a velocidade vx→, de módulo, direção e sentido constantes, dessa forma na horizontal teremos um movimento uniforme.
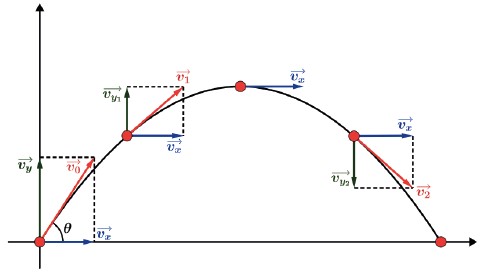
Decompondo a velocidade inicial de lançamento v0 → teremos

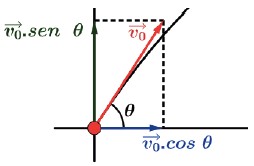

Vamos utilizar as equações horárias do movimento uniformemente variado para o movimento vertical.
No ponto de altura máxima a velocidade é nula e a velocidade vertical inicial do movimento é vy→.

Lembre-se que o tempo de subida é igual o tempo de descida e assim

Logo tempo total do movimento será

Pela equação de Torricelli teremos

Depois de encontrado o tempo total do movimento e fazendo a análise do movimento na horizontal teremos

Se utilizarmos vx → = v0 → · cos θ e vy → = v0 → · sen θ teremos

Exemplo: No instante t = 0, uma partícula é lançada de um ponto 0 do solo, com velocidade v0→ formando um ângulo θ com a horizontal.
São dados:

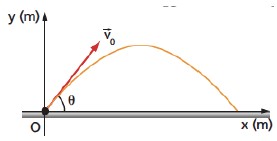
Desprezando os efeitos do ar e adotando um sistema de coordenadas com origem em O, como mostra a figura, pedem-se:
a) as equações horárias da abscissa x e da ordenada y da partícula;
b) a equação horária da componente vertical da velocidade;
c) as coordenadas da partícula no instante t = 6,0 s;
d) o módulo da velocidade da partícula no instante t = 18 s: nesse instante a partícula está subindo ou descendo?
e) a tangente do ângulo formado entre a velocidade e a direção horizontal no instante t = 18 s;
f) o instante em que a partícula atinge o vértice da trajetória;
g) o instante em que a partícula atinge o solo;
h) o alcance horizontal;
Resolução:
a) Teremos

No eixo x (horizontal) teremos um movimento uniforme
x = 50 t
No eixo y (vertical) teremos um movimento uniformemente variado

b) v = vy – gt ⇒ v= 120 – 10t
c) Teremos, para t = 6 s
x = 50t = 50 · 6 = 300 my =120t – 5t2 = 120 · 6 – 5 · 62 = 720 – 5 · 36 = 720 – 180 = 540 m
Para t = 6 s temos o ponto P(300,540)
d) Para t = 18 s teremos
v = 120 – 10t = 120 – 10 · 18 = 120 – 180 = – 60 m/s
Encontramos uma velocidade negativa, isso significa que a velocidade já se encontra com sentido contrário ao sentido suposto inicialmente, dessa forma a partícula está descendo.
e)
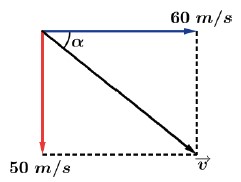

f) Nesse instante a velocidade vertical é nula
v = 120 – 10t ⇒ 0 = 120 – 10t ⇒ 10t = 120 ⇒ t = 12 s
g) O tempo total de movimento é o dobro do tempo de subida
ttotal = 2 · 12 = 24 s
h) Sendo o tempo total igual a 24 s teremos
A = 50t = 50 · 24 =1200 m
ALCANCE MÁXIMO
Será que se lançarmos uma partícula com a mesma velocidade inicial, mas sob ângulos de tiro diferentes será possível determinar um melhor ângulo de tiro? Encontraremos um ângulo onde o alcance horizontal da partícula será máximo?
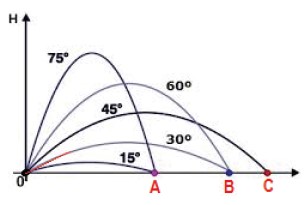
Vimos que o alcance em função da velocidade inicial de lançamento v0 pode ser escrito como

Da trigonometria temos que 2 · senθ · cosθ = sen2θ e assim

Sendo v0 invariável (depende da velocidade inicial do lançamento que uma vez a partícula lançada não poderá ser modificada) e a gravidade invariável o alcance variará de acordo com a função sen2θ. Como a função seno possui um valor máximo igual a 1 podemos determinar o ângulo θ capaz de maximizar sen2θ.
sen2θ = 1 ⇒ sen2θ = sen90 °⇒ 2θ = 90° ⇒ θ = 45°
Dessa forma percebemos que o ângulo de tiro capaz de produzir o máximo alcance é o ângulo de 45º.
Exercício Resolvido 1: (ACAFE SC) O puma é um animal que alcança velocidade de até 18 m/s e pode caçar desde roedores e coelhos até animais maiores como alces e veados. Considere um desses animais que deseja saltar sobre sua presa, neste caso um pequeno coelho, conforme a figura.
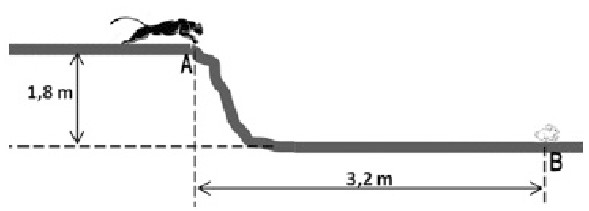
O puma chega ao ponto A com velocidade horizontal de 5 m/s e se lança para chegar à presa que permanece imóvel no ponto B. Desconsiderando a resistência do ar e adotando g = 10 m/s², a alternativa correta é:
a) O puma não vai cair sobre a presa, pois vai tocar o solo a 20 cm antes da posição do coelho.
b) O puma cairá exatamente sobre o coelho, alcançando sua presa.
c) O puma vai chegar ao solo, no nível do coelho, após 0,5 s do início de seu salto.
d) O puma vai cair 30 cm a frente do coelho, dando possibilidade de a presa escapar.
Resolução:
O tempo que o puma leva para cair é:

Dessa forma, seu alcance horizontal será de:
A = v0 · t = 5 · 0,6 ⇒ A = 3,0 m
Como a presa está a 3,2 m de distância, o puma cairá 20 cm antes dela.
Exercício Resolvido 2: Um corpo é lançado obliquamente com velocidade de módulo 60 m/s, sob um ângulo de lançamento θ = 60º (senθ = 0,87 e cosθ = 0,50), conforme indica a figura:
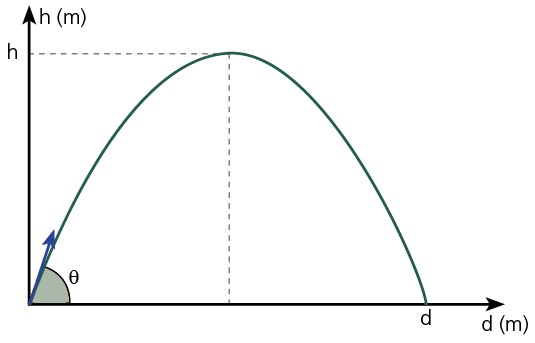
Calcular, considerando g = 10 m/s² e desprezando influências do ar:
a) a velocidade do corpo ao passar pelo vértice do arco de parábola;
b) o tempo de subida;
c) a altura máxima h;
d) o alcance horizontal d.
Resolução:
a) No vértice da parábola, há apenas a velocidade horizontal, já que a velocidade vertical é nula nesse ponto vx = v0 · cos(θ) = 60 · 0,5 ⇒ vx = 30,0 m/s





