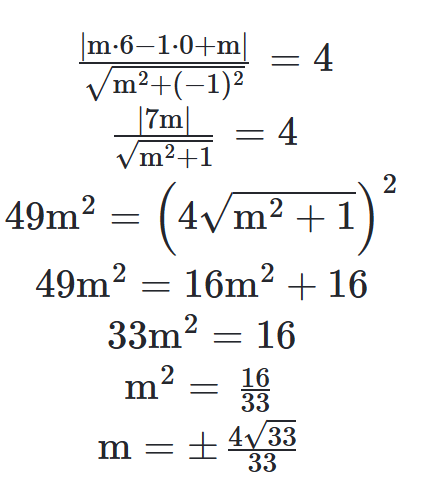RETA TANGENTE A CIRCUNFERÊNCIA
Sempre que desejamos encontrar a intersecção entre 2 curvas devemos resolver um sistema envolvendo as equações das 2 curvas. O sistema encontrado entre uma equação de circunferência e uma equação de reta seria:
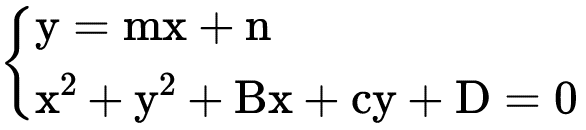
assim por substituição teremos:
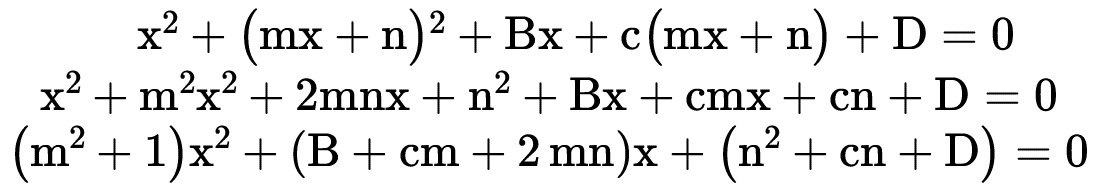
Logicamente isso não foi exposto para ser decorado mas sim para mostrar que todo sistema entre uma equação de reta e uma equação de circunferência resulta numa equação do 2° grau onde daí sabemos que
Δ > 0 → 2 pontos de intersecção → reta secante
Δ = 0 → 1 ponto de intersecção → reta tangente
Δ < 0 → Nenhum ponto de intersecção → reta exterior
Daí da equação (m2 + 1)x2 + (B + cm + 2mn)x + (n2 + cn +D) = 0 resultante do sistema basta fazermos o delta corresponde a situação de reta que nos for pedida.
Exemplo: Encontre a equação de reta que passa pelo ponto (-1, 0)e e é tangente a circunferência x2 + y2 − 12x + 20 = 0.
Reta y = mx + n que passa por (−1, 0) → 0 = m(−1) + n → m = n, assim y = mx + m.
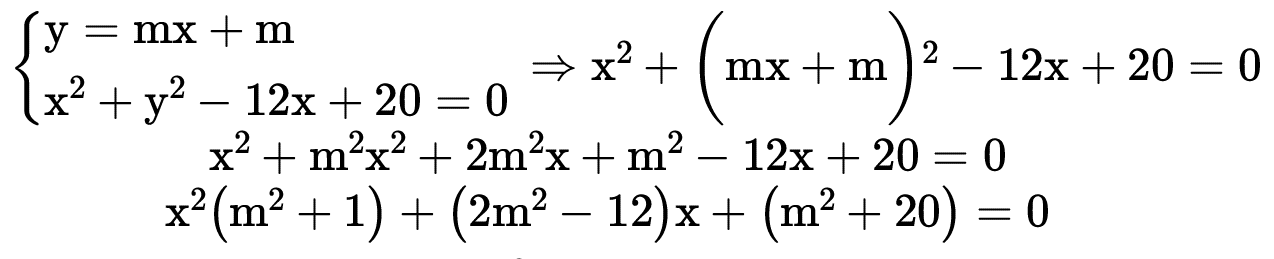
tangente Δ = 0 ⇒ (2m2 – 12)2 – 4 . (m2 + 1) . (m2 + 20) = 0
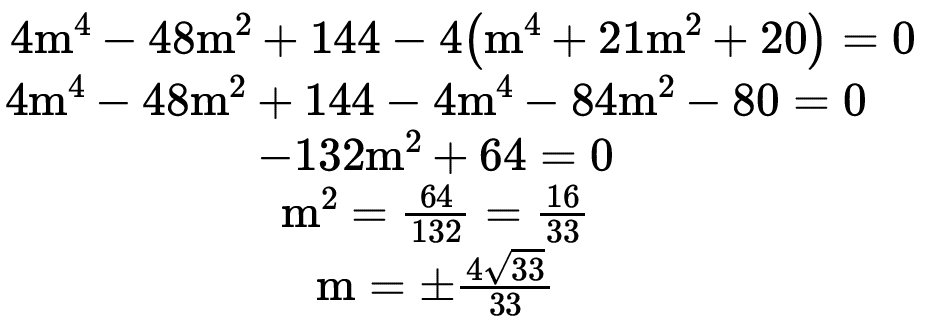
Assim nossas retas tangentes são:
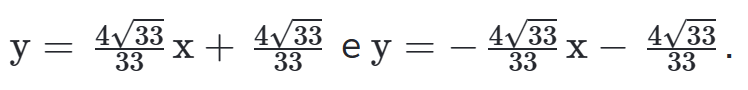
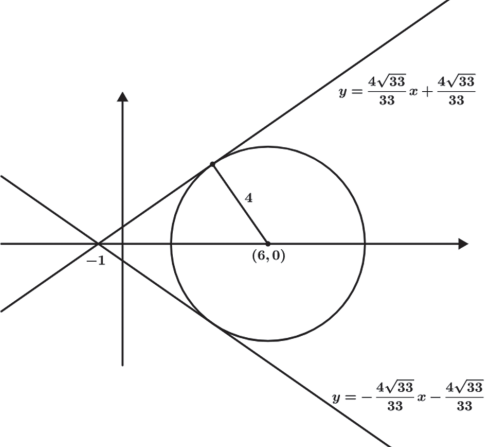
Também é possível encontrar a reta tangente utilizando a fórmula de distância de ponto a reta. Para isso devemos encontrar o centro e o raio da circunferência
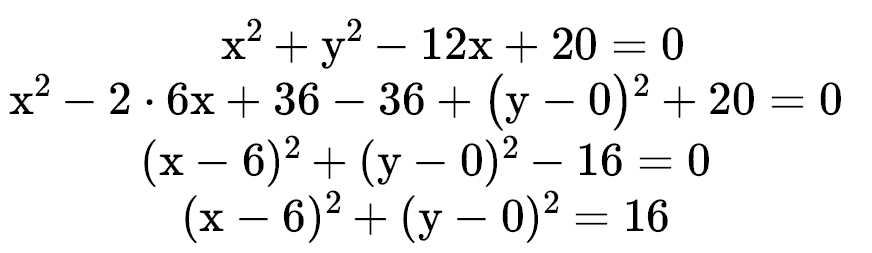
Centro (6, 0) e R2 = 16 ⇒ R = 4
A reta como vimos é y = mx + m ⇒ mx − y + m = 0.
Assim pela fórmula de distância de ponto a reta sendo a reta na sua forma completa e seus coeficientes a = m, b = -1 e c = m.